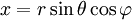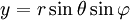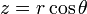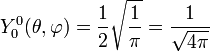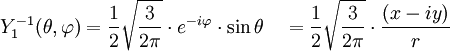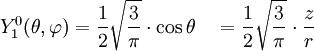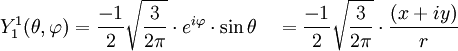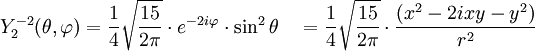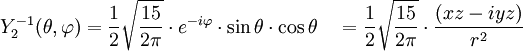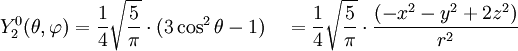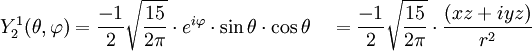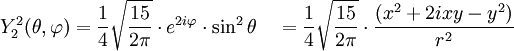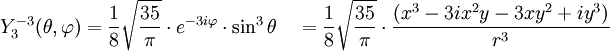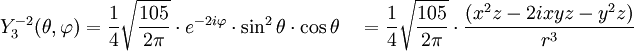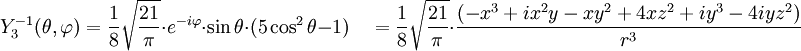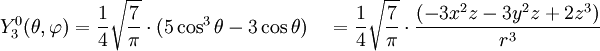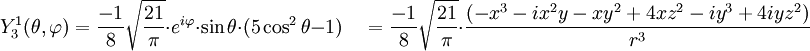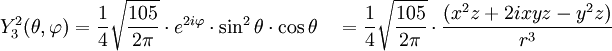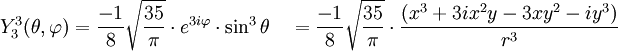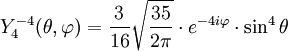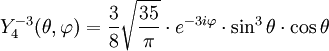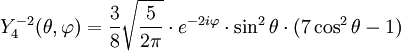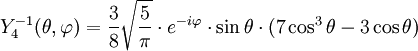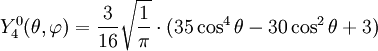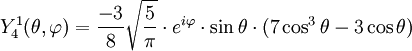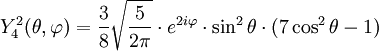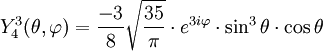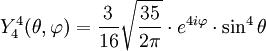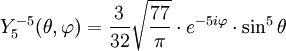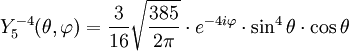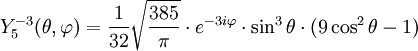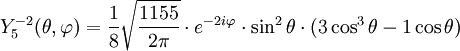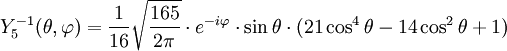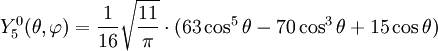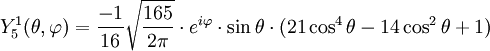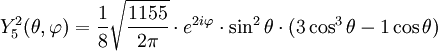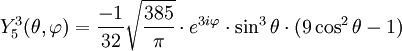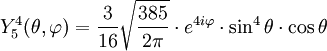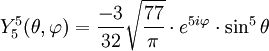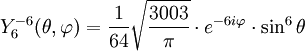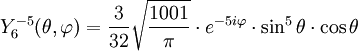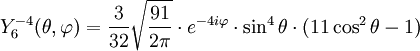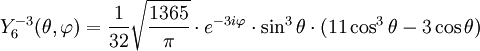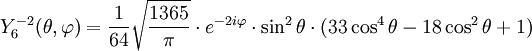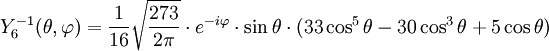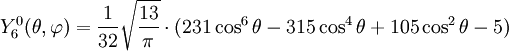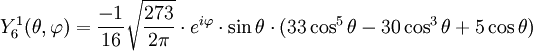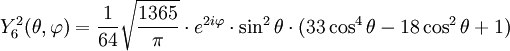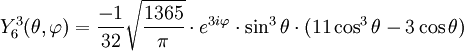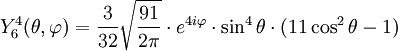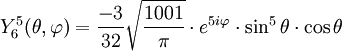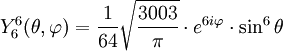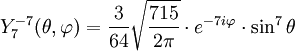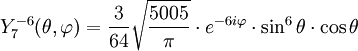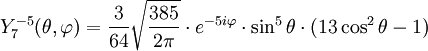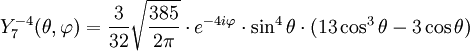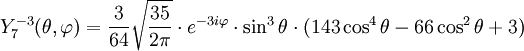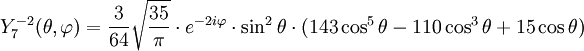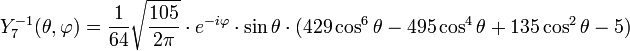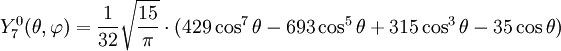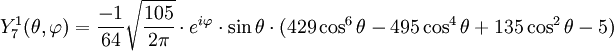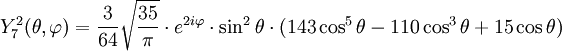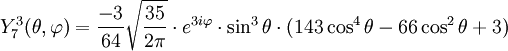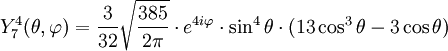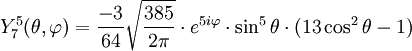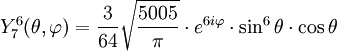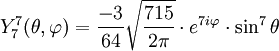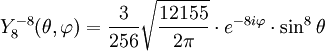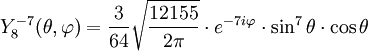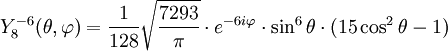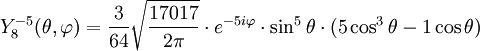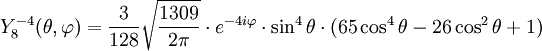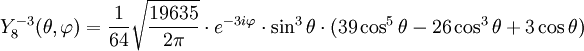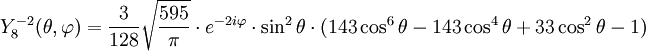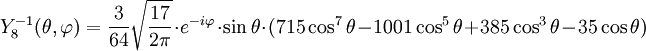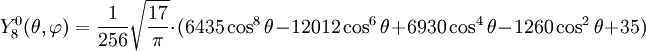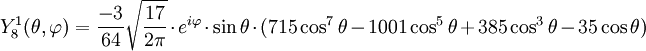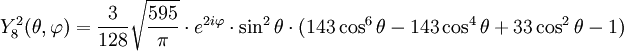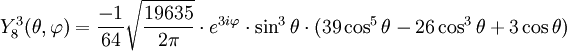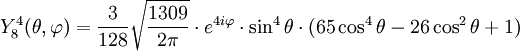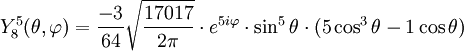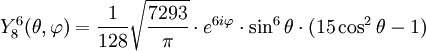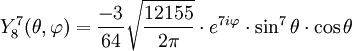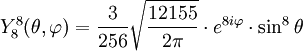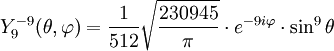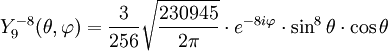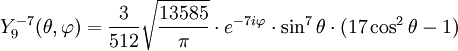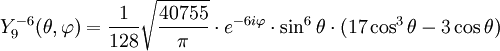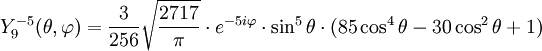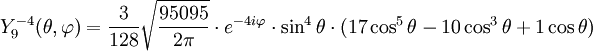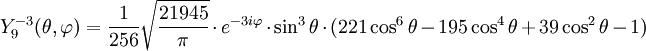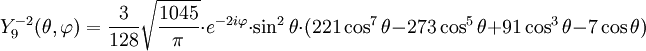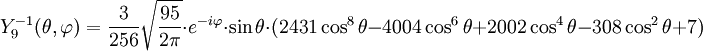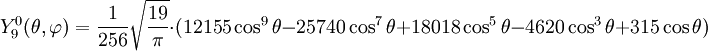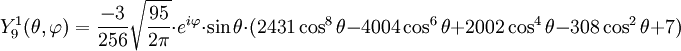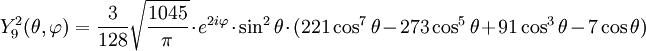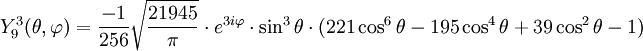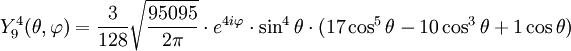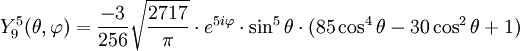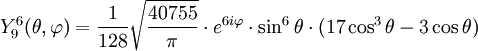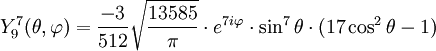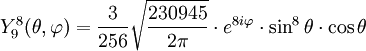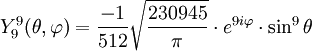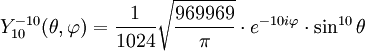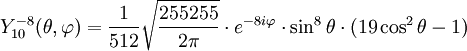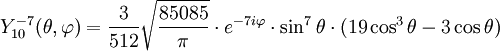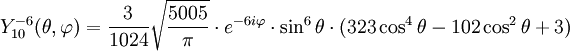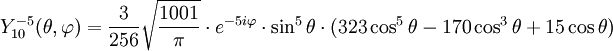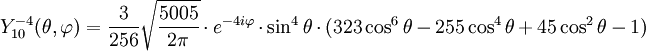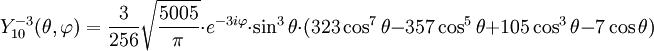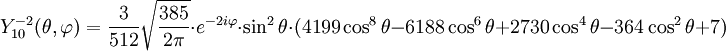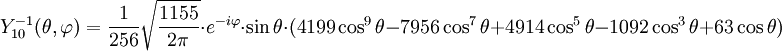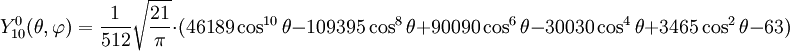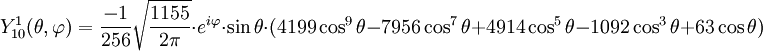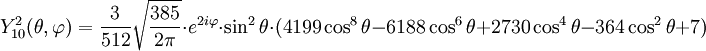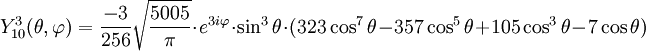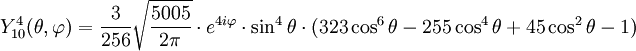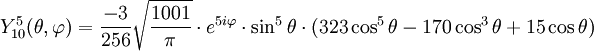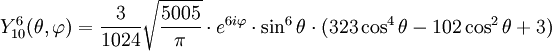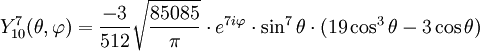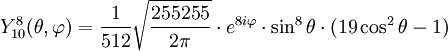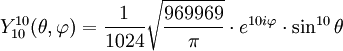Tabla de armónicos esféricos
- Tabla de armónicos esféricos
-
Anexo:Tabla de armónicos esféricos
Wikimedia foundation.
2010.
Mira otros diccionarios:
Anexo:Tabla de armónicos esféricos — Esta es una tabla de armónicos esféricos ortonormalizados que utilizan la convención de Condon Shortley para la fase, hasta el grado l=10. Algunas de estas fórmulas están dadas en su versión Cartesiana . En dichas coordenadas x, y, z, se… … Wikipedia Español
Armónicos esféricos — Saltar a navegación, búsqueda En matemáticas, los armónicos esféricos son funciones armónicas que representan la variación espacial de un conjunto ortogonal de soluciones de la ecuación de Laplace cuando la solución se expresa en coordenadas… … Wikipedia Español
Átomo de hidrógeno — Este artículo o sección tiene un estilo difícil de entender para los lectores interesados en el tema. Si puedes, por favor edítalo y contribuye a hacerlo más accesible para el público general, sin eliminar los detalles técnicos que interesan a… … Wikipedia Español
Configuración electrónica — Este artículo o sección necesita referencias que aparezcan en una publicación acreditada, como revistas especializadas, monografías, prensa diaria o páginas de Internet fidedignas. Puedes añadirlas así o avisar … Wikipedia Español
Orbital atómico — Orbitales atómicos y moleculares. El esquema de la izquierda es la regla de Madelung para determinar la secuencia energética de orbitales. El resultado es la secuencia inferior de la imagen. Hay que tener en cuenta que los orbitales son función… … Wikipedia Español
Coeficientes Clebsch—Gordan — Para los coeficientes vea el Anexo:Tabla de coeficientes de Clebsch Gordan. En física, los coeficientes Clebsch Gordan o coeficientes CG son el conjunto de números que aparecen al acoplar momentos angulares en mecánica cuántica. El nombre deriva… … Wikipedia Español
Átomo hidrogenoide — Los átomos hidrogenoides son átomos formados por un núcleo y un solo electrón. Se llaman así porque son isoelectrónicos con el átomo de hidrógeno y, por tanto, tendrán un comportamiento químico similar. Evidentemente, cualquiera de los isótopos… … Wikipedia Español
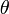 y
y 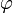 mediante el sistema usual de cambio de coordenadas:
mediante el sistema usual de cambio de coordenadas: