- Unión de conjuntos
-
 La unión de los conjuntos A y B es otro conjunto A ∪ B que contiene todos los elementos de A y de B.
La unión de los conjuntos A y B es otro conjunto A ∪ B que contiene todos los elementos de A y de B.
En la teoría de conjuntos, la unión de dos (o más) conjuntos es una operación que resulta en otro conjunto cuyos elementos son los elementos de los conjuntos iniciales. Por ejemplo, el conjunto de los números naturales es la unión del conjunto de los números pares positivos P y el conjunto de los número impares positivos I:
- P = {2, 4, 6, ...}
- I = {1, 3, 5, ...}
- N = {1, 2, 3, 4, 5, 6, ...}
La unión de conjuntos se denota por el símbolo ∪, de modo que por ejemplo, N = P ∪ I.
Contenido
Definición
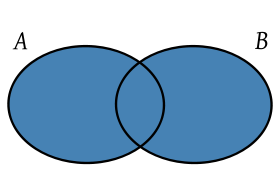 Unión de dos conjuntos A y B.
Unión de dos conjuntos A y B.
Dados dos conjuntos A y B, la unión de ambos, A ∪ B, es el conjunto que contiene todos los elementos de A y de B:
La unión de dos conjuntos A y B es otro conjunto A ∪ B cuyos elementos son todos los elementos de A o de B:

Ejemplo.
- Sean A = {a, ♠, 5} y B = {8, #}. La unión es A ∪ B = {5, #, a, ♠, 8}.
- Considerando los conjuntos de números naturales C = {n: n es un número primo} y D = {m: m es un número compuesto}. La unión es entonces (C ∪ D) = {n: n es primo o compuesto} = {2, 3, 4, 5, ...}, ya que el único número natural que no es ni primo ni compuesto es (por definición) 1.
En la unión de conjuntos, los elementos repetidos sólo aparecen una vez, pues los conjuntos no pueden tener elementos repetidos:[n 1]
- La unión de {1, 2, 3, 4, 5} y {6, 2, 9, 1} es {1, 2, 3, 4, 5, 6, 9}.
Generalizaciones
Es posible definir la unión de un número finito de conjuntos, superior a dos:

Y la unión se puede calcular utilizando la propiedad asociativa de la unión (más abajo). De este modo, para unir varios conjuntos el orden en el que se haga es irrelevante:

Una definición más general en teoría de conjuntos se refiere a una familia de conjuntos:
Sea M una familia de conjuntos. Su unión ∪M se define como:

De este modo, la unión de un número finito de conjuntos es sólo un caso particular de la definición general anterior.
- A ∪ B = ∪M, donde M = {A, B}
- A1 ∪ ... ∪ An = ∪M, donde M = {A1, ..., An}
La unión general de conjuntos se denota de diversas maneras:

donde esta última se aplica en el caso de que utilicemos un conjunto índice, tomando M como {Ai: i ∈ I}.
Propiedades
De la definición de unión puede deducirse directamente:
- Idempotencia. La unión de un conjunto A consigo mismo es el propio A :
- A ∪ A = A
- Tanto A como B son subconjuntos de su unión:
- A ⊆ A ∪ B y B ⊆ A ∪ B
- La unión de un conjunto A con un subconjunto suyo B lo deja inalterado:
- B ⊆ A implica que A ∪ B = A
La unión de conjuntos posee también propiedades similares a las operaciones con números:
- Propiedad asociativa. La unión de los conjuntos A y B ∪ C es igual que la unión de los conjuntos A ∪ B y C :
- (A ∪ B) ∪ C = A ∪ (B ∪ C)
- Propiedad conmutativa. La unión de los conjuntos A y B es igual a la unión de los conjuntos B y A :
- A ∪ B = B ∪ A.
- Elemento neutro. La unión de un conjunto A con el conjunto vacío ∅ es el mismo conjunto A:
- A ∪ ∅ = A
Todas estas propiedades se deducen de propiedades análogas para la disyunción lógica.
En relación con la operación de intersección existen unas leyes distributivas:
- A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C), y por tanto:
- A ∪ (A ∩ B) = A
- A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C), y por tanto:
- A ∩ (A ∪ B) = A
Cardinalidad
El número de elementos de la unión de dos conjuntos finitos A y B es la suma de los elementos de A y de B, si no tienen elementos en común.
Si A y B son conjuntos disjuntos:

Como en un conjunto los elementos no pueden repetirse, si A y B tienen elementos en común, al sumar sus elementos se contarían los elementos comunes más de una vez. Por ejemplo:
- {1, a, ♠} y {b, a, 5} tienen ambos tres elementos, pero su unión {1, a, ♠, b, 5} tiene cinco elementos y no seis.
Por ello, es necesario eliminar las repeticiones al contar los elementos de A ∪ B:
Dados dos conjuntos finitos A y B :

Esta fórmula se generaliza para el caso más complicado de una unión de un número arbitrario de conjuntos finitos. Por ejemplo en el caso de tres conjuntos se tiene:
- |A ∪ B ∪ C| = |A| + |B| + |C| − |A ∩ B| − |B ∩ C| − |C ∩ A| + |A ∩ B ∩ C|
y en general se tiene el llamado principio de inclusión-exclusión:
Dada una colección finita de conjuntos A1, ..., An :

Todas estas fórmulas se demuestran con facilidad para el caso en el que los conjuntos involucrados sean finitos. Sin embargo, también son ciertas en el caso de conjuntos infinitos, aunque requieren el uso de cardinales infinitos.
Axioma de la unión
En teoría axiomática de conjuntos no puede demostrarse la existencia de la unión de conjuntos a partir de propiedades más básicas. Es por ello que se postula la existencia de la unión, añadiendo como axioma el llamado axioma de unión.
Referencias
- ↑ A diferencia de los multiconjuntos, que sí permiten repeticiones.
- Dorronsoro, José; Hernández, Eugenio (1996). Números, grupos y anillos. Addison-Wesley/Universidad Autónoma de Madrid. ISBN 84-7829-009-5.
- Matoušek, Jiří; Nešetřil, Jaroslav (2008). Invitación a la matemática discreta. Reverte. ISBN 9788429151800.
- Lipschutz, Seymour (1991). Teoría de conjuntos y temas afines. McGraw-Hill. ISBN 968-422-926-7.
Véase también
Wikimedia foundation. 2010.
