- Vector de Runge-Lenz
-
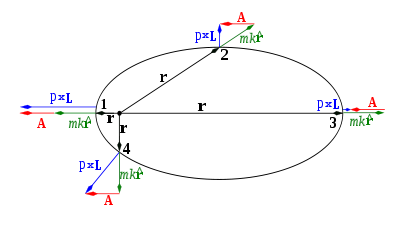 Figura 1: El vector de RL A (en rojo) para cuatro puntos (marcados como 1, 2, 3 y 4) sobre la órbita elíptica de un planeta que se mueve bajo la acción de una fuerza central que sigue la ley de la inversa del cuadrado. En centro de atracción se smarca como un pequeño círculo negro a partir del cual se consideran que emanan los vectores posición (en negro). El momento angular L es perpendicular a la órbita. Los vectores coplanarios p×L y (mk/r)r se muestran en azul y en verde, respectivamente. Estas variables se definen más adelante en este artículo. El vector A es constante en dirección y magnitud.
Figura 1: El vector de RL A (en rojo) para cuatro puntos (marcados como 1, 2, 3 y 4) sobre la órbita elíptica de un planeta que se mueve bajo la acción de una fuerza central que sigue la ley de la inversa del cuadrado. En centro de atracción se smarca como un pequeño círculo negro a partir del cual se consideran que emanan los vectores posición (en negro). El momento angular L es perpendicular a la órbita. Los vectores coplanarios p×L y (mk/r)r se muestran en azul y en verde, respectivamente. Estas variables se definen más adelante en este artículo. El vector A es constante en dirección y magnitud.
El vector de Runge-Lenz (o vector de Laplace-Runge-Lenz) es una constante de movimiento del problema de los dos cuerpos en interacción gravitatoria mutua. La existencia de esta integral de movimiento es una de las formas más simples de probar que las trayectorias planetarias en ese caso son cónicas.
Contenido
Motivación
El vector de Runge-Lenz aparece de manera natural a partir de la ecuación de movimiento. Si tomanos un sistema de referencia inercial con origen en el centro de masas y consideramos las distancias relativas de los dos cuerpos o astros respecto a él, podemos definir el vector diferencia:

Donde los dos vectores que aparecen en segundo término son los vectores de posición del primer y segundo cuerpo respectivamente. En términos del vector diferencia la ecuación de movimiento puede expresarse como:
(1) No se pudo entender (La conversión a PNG ha sido errónea): \ddot\mathbf{r} = -\mu\frac{\mathbf{r}}{r^3}
Donde μ = G(m1+m2). La existencia de una constante adicional además de la energía y el momento angular puede probarse muy fácilmente a partir de (). Si se multiplica por la velocidad se obtiene:
No se pudo entender (La conversión a PNG ha sido errónea): \mathbf{r} \times \dot\mathbf{r} = \mathbf{0}
Que se puede integrar sin dificultad:
No se pudo entender (La conversión a PNG ha sido errónea): \mathbf{r} \times \dot\mathbf{r} = \mathbf{l} = \mbox{cte.}
Esta vector constante de hecho coincide con el momento angular por unidad de masa, y puede calcularse sin dificultad a partir de los datos iniciales. Si multiplicamos este vector constante por la aceleración nuevamente y hacemos algunas manipulaciones algebraicas tenemos:
No se pudo entender (La conversión a PNG ha sido errónea): \mathbf{l} \times \ddot\mathbf{r} = -\frac{\mu}{r^3}\mathbf{l} \times \mathbf{r} = -\frac{\mu}{r^3}[(\mathbf{r} \times \dot\mathbf{r}) \times \mathbf{r}] = -\frac{\mu}{r^3}[r^2 \dot\mathbf{r} - (\dot\mathbf{r}\cdot\mathbf{r})\mathbf{r}] = -mu\left[\frac{\dot\mathbf{r}}{r}-\frac{\dot{r}}{r^2}\mathbf{r}\right] = \mu\frac{d}{dt}\left( \frac{\mathbf{r}}{r} \right)
De esta última igualdad reordenando términos se tiene que:
(2) No se pudo entender (La conversión a PNG ha sido errónea): \frac{d}{dt}\left(\mathbf{l} \times \ddot\mathbf{r} - \mu \frac{\mathbf{r}}{r}\right) = 0 \qquad \Rightarrow \qquad \mathbf{A} = \left(\mathbf{l} \times \ddot\mathbf{r} - \mu \frac{\mathbf{r}}{r}\right) = \mbox{cte.}
Y es este vector
 el que se conoce como vector (Laplace-)Runge-Lenz.
el que se conoce como vector (Laplace-)Runge-Lenz.Propiedades
- El vector de Runge-Lenz está contenido en el plano de la órbita.
- Además el vector de Runge-Lenz coincide con uno de los semiejes de la cónica
- El módulo del vector de Runge-Lenz de μ > 0 coincide con el valor absoluto de la excentricidad.
- Las componentes del vector de Runge-Lenz no son todas independientes ya que cumplen la relación

Forma de la órbita
De la conservación del vector Runge-Lenz, (), se sigue que la forma de la órbita en el problema de Kepler es una cónica,[1] para verlo basta multiplicar dicho vector escalarmente por el vector posición, para obtener que:
No se pudo entender (La conversión a PNG ha sido errónea): \begin{cases} -\mathbf{r} \cdot (\mathbf{l}\times\dot\mathbf{r}) = \mu r + \mathbf{A}\cdot\mathbf{r},\\ \mathbf{l} \cdot (\mathbf{r}\times\dot\mathbf{r}) = \mu r + \mathbf{A}\cdot\mathbf{r} \end{cases} \qquad \Rightarrow \qquad \|\mathbf{l}\|^2 = l^2 = \mu r+\mathbf{A}\cdot\mathbf{r}
Si la fuerza es atractiva (μ > 0) podemos reescribir la última expresión como:
(3) No se pudo entender (La conversión a PNG ha sido errónea): \frac{l^2}{r} = \mu + \mathbf{A}\cdot\hat\mathbf{r} = \mu (1 + e\cos \varphi) \qquad \Rightarrow \qquad \frac{p}{r} = 1 + e\cos \varphi
Donde e es la excentricidad de la órbita, y p = l2/μ es el semilatus rectum de la elipse, cuya ecuación en coordenadas polares viene dada por ().
Referencias
- ↑ Rañada, 2005, p.304.
- Fernández Rañada, Antonio. Fondo de Cultura Económica. ed. Dinámica Clásica (1ª edición). México DF. pp. 302-304. ISBN 84-206-8133-4.
Categorías:- Mecánica clásica
- Simetría rotacional
- Vectores
Wikimedia foundation. 2010.
