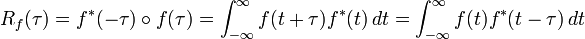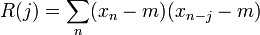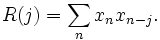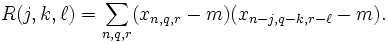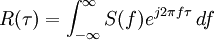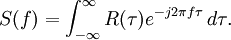- Autocorrelación
-
Autocorrelación
La autocorrelación es una herramienta matemática utilizada frecuentemente en el procesado de señales.
La función de autocorrelación se define como la correlación cruzada de la señal consigo misma. La función de autocorrelación resulta de gran utilidad para encontrar patrones repetitivos dentro de una señal, como por ejemplo, la periodicidad de una señal enmascarada bajo el ruido o para identificar la frecuencia fundamental de una señal que no contiene dicha componente, pero aparecen numerosas frecuencias armónicas de esta.
Contenido
Definiciones de la función de autocorrelación
Dependiendo del campo de estudio se pueden definir diferentes tipos de autocorrelación sin que estas definiciones sean equivalentes. En algunos campos se utilizan indistintamente las funciones de autocorrelación y de autocovarianzas, dado que ambas sólo difieren entre sí en una constante de proporcionalidad que es la varianza (en este caso, la autocovarianza de orden k=0).
Estadística
En estadística, la autocorrelación de una serie temporal discreta de un proceso Xt es simplemente la correlación de dicho proceso con una versión desplazada en el tiempo de la propia serie temporal.
Si Xt representa un proceso estacionario de segundo orden con un valor principal de μ se define entonces:
donde E es el valor esperado y k el desplazamiento temporal considerado (normalmente denominado desfase). Esta función varía dentro del rango [−1, 1], donde 1 indica una correlación perfecta (la señal se superpone perfectamente tras un desplazamiento temporal de k) y −1 indica una anticorrelación perfecta. Es una práctica común en muchas disciplinas el abandonar la normalización por σ2 y utilizar los términos autocorrelación y autocovarianza de manera intercambiable.
Procesamiento de señales
En el procesamiento de señales, dada una señal temporal f(t), la autocorrelación continua Rf(τ) es la correlación continua cruzada de f(t) consigo mismo tras un desfase τ, y se define como:
donde f * representa el conjugado complejo y el círculo representa una convolución. Para una función real, f * = f.
Formalmente, la autocorrelación discreta R con un desfase j para una señal xn es
donde m es el valor esperado de xn.
Frecuentemente las autocorrelaciones se calculan para señales centradas alrededor del cero, es decir con un valor principal de cero. En ese caso la definición de la autocorrelación viene dada por:
Las autocorrelaciones multidimensionales pueden definirse de manera similar. Por ejemplo, en tres dimensiones puede definirse la autocorrelación de una función como:
Propiedades
Definiremos las propiedades de la autocorrelación unidmensional. La mayoría de sus propiedades son extensibles fácilmente a los casos multidimensionales.
- Simetría: R(i) = R(−i),
- La función de autocorrelación alcanza un valor máximo en el origen, donde alcanza un valor real. El mismo resultado puede encontrarse en el caso discreto.
- Como la autocorrelación es un tipo específico de correlación mantiene todas las propiedades de la correlación.
- La autocorrelación de una señal de ruido blanco tendrá un fuerte pico en τ = 0 y valores cercanos a cero y sin ninguna estructura para cualquier otro τ . Esto muestra que el ruido blanco carece de periodicidad.
- Según el teorema de Wiener-Khinchin, la función de autocorrelación es la transformada inversa de Fourier de la densidad espectral:
Igualmente, el espectro se relaciona con la función de autocorrelación:
La consecuencia es que la señal puede expresarse indistintamente en el dominio del tiempo (t) o el dominio de las frecuencias (f), al existir esta correspondencia entre ambos, y entendiendo que la señal está completamente determinada a partir del total de sus momentos o del total de sus frecuencias.
Aplicaciones
- Una de las aplicaciones de la autocorrelación es la medida de espectros ópticos y en especial la medida de pulsos muy cortos de luz.
- En óptica, la autocorrelación normalizada y la correlación cruzada proporcionan el grado de coherencia de un campo electromagnético.
- En el procesamiento de señales, la autocorrelación proporciona información sobre las periodicidades de la señal y sus frecuencias características como los armónicos de una nota musical producida por un instrumento determinado (tono y timbre).
Enlaces externos
- MathWorld: Autocorrelation (en inglés)
- Autocorrelation articles in Comp.DSP (DSP usenet group). (en inglés)
Categorías: Análisis armónico | Análisis de la regresión | Covarianza y correlación
Wikimedia foundation. 2010.

![R(k) = \frac{E[(X_i - \mu)(X_{i+k} - \mu)]}{\sigma^2}](/pictures/eswiki/98/b649019848cf9ea45681a1f74712992a.png)