Autómata probabilístico

Autómata probabilístico

Saltar a navegación, búsqueda

Un autómata probabilístico es una generalización del automáta finito no determinista; incluye la probabilidad de una transición dada de una función de transición, convirtiéndola en una matriz de transición.

Definición

Los autómatas probabilísticos nos permiten tener una idea de cómo la transición entre estados de un autómata puede no ser factible (probabilidad 1) sino que puede llegar a existir una probabilidad asociada a que se realice una determinada transición. Por lo tanto no podemos estar seguros de que el autómata se encuentre en un determinado estado en cierto momento solo podemos llegar a saber la probabilidad de que esto suceda. Los autómatas probabilísticos se definen con una quintupla:

AFP = (Σ, Q, M, P (0), F)

Donde:

• Σ es el alfabeto de los símbolos de entrada.
• Q es el conjunto de estados.
• M es el conjunto de matrices de probabilidad de transición entre estados,
• M = {M (a)|a Є Σ}.
• P (0) es el vector de estado inicial.
• F Í Q es el conjunto de estados finales.

En los AFP por cada símbolo del alfabeto tenemos una matriz de probabilidad, la cual la podemos definir formalmente como:

Aplicaciones

Existen muchas aplicaciones que hacen uso de este tipo de AFP como puede ser:

Reconocimiento de voz

Cuando una persona habla a un micrófono el sistema puede generar como salida las palabras dichas por esta persona, para ello se hace uso de AFP llamadas cadenas de Márkov. Por poner un ejemplo si después de una a tenemos un 10 % de probabilidades de tener una d y un 1 % de tener una e, el autómata se construirá tendrá en cuenta estas probabilidades para su funcionamiento y reconocimiento de los caracteres.

Robótica

Cuando un robot está en movimiento y quiere saber lo que le rodea se hacen uso de los AFP ya que los sensores siempre pueden tener un error, o existir un rozamiento en las ruedas que afecte a su percepción de los elementos que le rodean, etc. Podemos implementar en los robots un AFP para según los elementos que le rodean y las consecuencias de las acciones del robot en el entorno, este actúe de una forma u otra.

Matrices de probabilidad de transición

Por cada símbolo de la matriz de entrada Σ existe un matriz de probabilidad M (a), que nos muestra la probabilidad de que un estado reciba un determinado símbolo y pueda pasar a otro estado.w---D

$\left( \begin{array}{cccc} p_{11} & p_{12} & \ldots & p_{1n}\\ \vdots & \ddots & & \vdots\\ p_{n1} & p_{n2} & \ldots & p_{nn}\end{array} \right)$

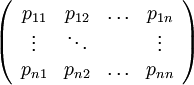
Donde:

• n es el número de estados, n = |Q|;
• p_ij es la probabilidad de que estando en el estado i y recibiendo una a como entrada, transite al estado j;
• para cada p_ij, se cumple 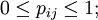$0 \leq p_{ij} \leq 1;$ y
• para cada estado i, $\sum^n_{j=1} p_{ij} = 1$.

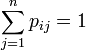Vectores de estados

El vector de estados en un instante de tiempo t, P(t) tiene un componente por cada estado y el contenido de cada estado dado por la posición i del vector P_i(t), y esto muestra la probabilidad de autómata en estar en ese estado i en el momento t.
La fórmula de cálculo para el vector completo será:

Pi(t + 1) = P(t) * M(a).

Lenguaje aceptado por un AFP

A veces necesitamos saber si un autómata acepta o no una determinada palabra, para ello hacemos uso de lo que vamos a conocer como umbral.

Cuanto mayor sea el umbral, más restrictivo será el AFP ya que este aceptará menos palabras.

El lenguaje aceptado por dicho AFP será todas las palabras cuyas transiciones lleven a algún estado final con una probabilidad mayor o igual que el umbral.

AF como AFP

Los Autómatas Finitos Deterministas y No Deterministas son un caso particular de AFP, en el que las probabilidades son 0 ó 1. Si se tiene un AFD = (Σ, Q, f, P (0), F, q), se puede obtener el AFP equivalente:

AFP = (Σ, Q, M, P (0), F, q)

Donde:

• el vector inicial debe de reflejar la idea de que sólo se está inicialmente en un estado q₀ y en ninguno más. Por tanto,

P_i(0) = 1 si i = q₀,

0 en caso contrario

• todas las transacciones permitidas por la función de transición f tienen probabilidad igual a 1, mientras que las que no se producen, tienen probabilidad igual a 0. Por tanto, para cada símbolo $a \in \Sigma$

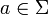
M_ij(a) = 1 si f(i,a) = j

0 en caso contrario

• el umbral debe ser mayor que cero, siendo válido cualquier valor.

Obtenido de "Aut%C3%B3mata probabil%C3%ADstico"