Construcción de subconjuntos

En teoría de la computación, la Construcción de subconjuntos es un método estándar para, partiendo de un NFA (Autómata Finito No Determinista), obtener un DFA (Autómata Finito Determinista) equivalente, es decir, que reconozca el mismo Lenguaje regular. En la teoría es importante porque establece que los NFAs aunque son más flexibles, no pueden reconocer ningún lenguaje que un DFA no pueda. Sin embargo, dado un NFA con n estados, el DFA equivalente podría tener hasta 2ⁿ estados, por lo que a veces, construir un DFA a partir de un NFA de gran tamaño no es practicable. Este problema se minimiza en gran medida con el algoritmo de Construcción de subconjuntos, el cual limita la inserción de estados al DFA resultante únicamente a los casos estrictamente necesarios.

Sea $M \equiv (Q, \Sigma, \delta, q_0, F)$ un NFA. El algoritmo de Construcción de subconjuntos permite hallar un DFA $M' \equiv (Q', \Sigma, \delta', q'_0, F')$ de modo que L(M) = L(M')

Algoritmo de construcción de subconjuntos

Veamos un Pseudocódigo para el algoritmo:

q'0 = S = $\epsilon-clausura(q_o)$;
desmarcar(S);
DFA_states := {S};
While ($\exists$ T $\in$ DFA_states and !marcado(T)) do
   marcar (T);
   For all a $\in \Sigma$ do
      R := $\epsilon-clausura(\delta$(T, a));
      δ'(T, a) := R;
      if (!(R $\in$ DFA_states)) then
         DFA_states := DFA_states $\cup$ {R};
         desmarcar(R);
      end;
  end;
end;

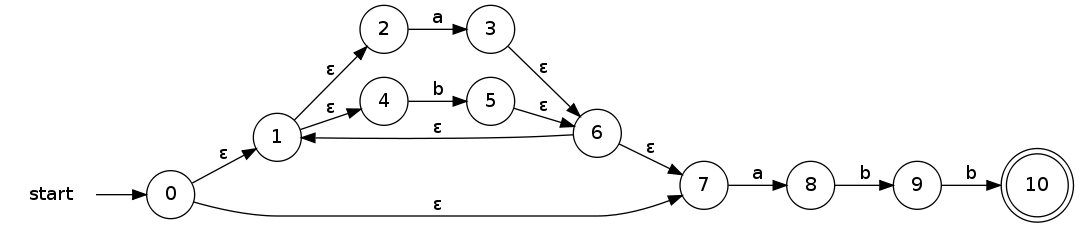
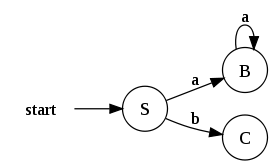
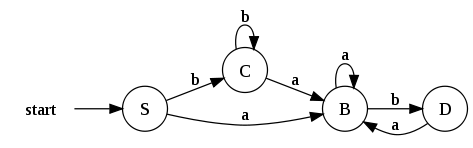
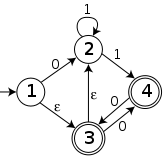
Apliquemos ahora el algoritmo al NFA de la siguiente figura:

Empezamos obteniendo la $\epsilon$-clausura del estado de arranque del NFA, es decir, el conjunto de estados alcanzables desde el estado inicial, consumiendo únicamente $\epsilon$-transiciones.

$\epsilon-clausura(0) = \{ 0, 1, 2, 4, 7\} = S = q'_0 \,$

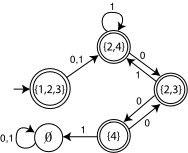
Una vez que tenemos definido el estado de arranque de nuestro DFA, podemos empezar a completar los estados y transiciones restantes. Como sabemos que S representa un conjunto de estados del NFA inicial, sólo tenemos que hacer transitar dicho conjunto con cada símbolo de nuestro alfabeto y estudiar a que otros conjuntos se llega. Si estos otros conjuntos no pertenecen a Q', entonces los añadiremos a nuestro DFA, en el caso contrario, sólo tendremos que añadir nuevas transiciones.
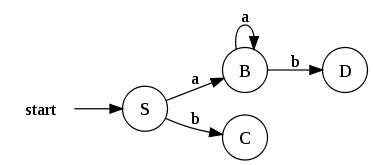
En nuestro caso, nuestro estado inicial S = {0,1,2,4,7} transita con símbolo 'a' a un nuevo conjunto ({3,8}), al cual calcularemos su $\epsilon$-clausura para obtener B = {0,1,2,3,4,6,7,8}.

$\delta(S, \, a) = \{3, 8\}$
$\epsilon -clausura(\{3, 8\}) = \{ 0, 1, 2, 3, 4, 6, 7, 8\} = B \Rightarrow \delta' (S,a)= B$

Repetimos el proceso anterior usando ahora el otro símbolo perteneciente a nuestro alfabeto.

$\delta(S, \, b) = \{5\}$
$\epsilon -clausura(\{5\}) = \{ 0, 1, 2, 4, 5, 6, 7\} = C \Rightarrow \delta' (S,b)= C$

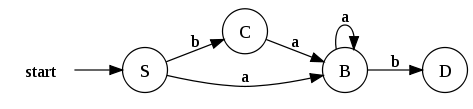
Una vez creadas todas las transiciones posibles para nuestro estado inicial (S), continuamos la ejecución del algoritmo con cada uno de los estados encontrados previamente. En esta iteración, obtenemos un conjunto de estados ya conocido, por lo cual, solo tendremos que añadir la transición correspondiente a nuestro autómata.

$\delta(B, \, a) = \{3, 8\}$
$\epsilon-clausura(\{3, \, 8\}) = B \Rightarrow \delta'(B, \, a)= B$

$\delta(B, \, b) = \{5, 9\}$
$\epsilon-clausura(\{5, 9\}) = \{1, 2, 4, 5, 6, 7, 9\} = D \Rightarrow \delta'(B, \, b) = D$

$\delta(C, \, a) = \{3, 8\}$
$\epsilon-clausura(\{3, 8\}) = B \Rightarrow \delta'(C, \, a)= B$

$\delta(C, \, b) = \{5\}$
$\epsilon-clausura(\{5\}) = C \Rightarrow \delta'(C, \, b) = C$

$\delta(D, \, a) = \{3,8\}$
$\epsilon-clausura(\{3,8\}) = B \Rightarrow \delta'(D, \, a)= B$

$\delta(D, \, b) = \{5, 10\}$
$\epsilon-clausura(\{5, 10\}) = \{1, 2, 4, 5, 6, 7, 10\}= E \Rightarrow \delta'(D, \, b)= E$

$\delta(E, \, a) = \{3, 8\}$
$\epsilon-clausura(\{3, 8\}) = B \Rightarrow \delta'(E, \, a)= B$

$\delta(E, \, b) = \{5\}$
$\epsilon-clausura(\{5\}) = C \Rightarrow \delta'(E, \, b) = C$

El conjunto de estados de aceptación del DFA resultante estará formado por todos aquellos estados que contengan un estado final del NFA. En nuestro caso, el NFA inicial tenía un estado de aceptación identificado como 10. En el proceso que hemos seguido sólo hemos obtenido un conjunto que contenga éste estado (E), por lo cual este se convertirá en nuestro nuevo estado de aceptación.

$F' = \{q \in Q' \,| \,q \cap F \neq \empty \}$

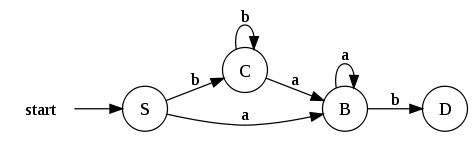
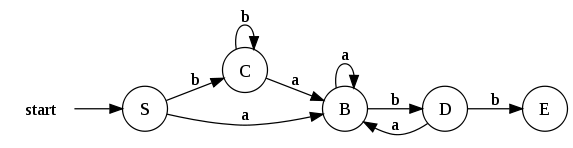
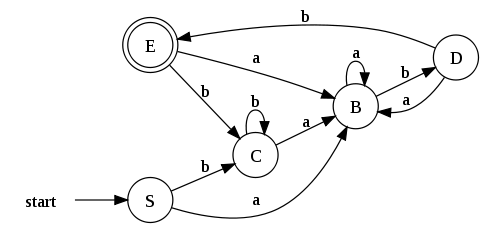
El DFA resultante quedaría de esta forma:

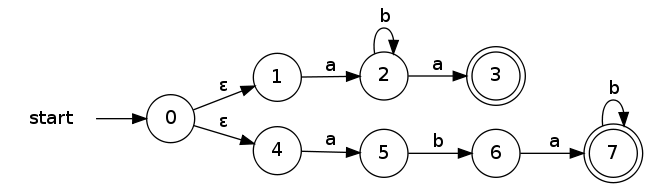
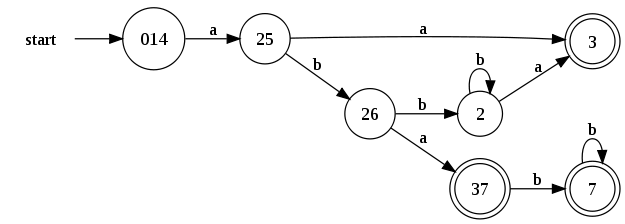
Otro ejemplo

Otro ejemplo

$\Downarrow$

Referencias

• Kelley, Dean (1995). Teoría de Autómatas y Lenguajes Formales. Prentice Hall. ISBN 0-13-518705-2. 
• Hopcroft, J., Motwani, R., y Ullman, J. (2002). Introducción a la teoría de Autómatas, Lenguajes y Computación. Addison Wesley. ISBN 84-7829-056-7. 

Enlaces externos

• Wikimedia Commons alberga contenido multimedia sobre Construcción de subconjuntos. Commons
• JFLAP, software para experimentar con lenguajes formales y autómatas