- Logaritmo natural
-
Logaritmo natural 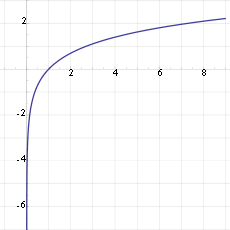
Gráfica de Logaritmo naturalDefinición 
Tipo Función real Descubridor(es) Nikolaus Mercator (1668)[1] Dominio 
Codominio 
Imagen 
Propiedades Biyectiva
Cóncava
Estrictamente creciente
Continua
TrascendenteCálculo infinitesimal Derivada 
Función inversa 
Límites 

Funciones relacionadas Logaritmo
Función exponencialEl logaritmo natural suele ser conocido normalmente como logaritmo neperiano, aunque esencialmente son conceptos distintos. Para más detalles, véase logaritmo neperiano.
En matemáticas se denomina logaritmo natural o informalmente logaritmo neperiano al logaritmo cuya base es el número e, un número irracional cuyo valor aproximado es 2,718281... El logaritmo natural se le suele denominar como ln(x) o a veces como loge(x) , porque para ese número se cumple la propiedad de que el logaritmo vale 1.
El logaritmo natural de un número x es entonces el exponente a al que debe ser elevado el número e para obtener x. Por ejemplo, el logaritmo de 7,38905... es 2, ya que e2=7,38905... El logaritmo de e es 1, ya que e1=e.
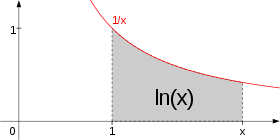
Desde el punto de vista del análisis matemático, puede definirse para cualquier número real positivo x>0 como el área bajo la curva y=1/t entre 1 y x. La sencillez de esta definición es la que justifica la denominación de "natural" para el logaritmo con esta base concreta.[2] Esta definición puede extenderse a los números complejos.
El logaritmo natural es entonces una función real con dominio de definición los números reales positivos:
y corresponde a la función inversa de la función exponencial:
Contenido
Historia
La primera mención del logaritmo natural fue dada por Nikolaus Mercator en su trabajo Logarithmotechnia publicado en 1668,[1] a pesar de que el profesor de matemáticas John Speidell ya lo había hecho en 1619 recopilando una tabla sobre valores del logaritmo natural.[3] Fue llamado formalmente como logaritmo hiperbólico,[4] puesto que sus valores correspondían con los del área hallada bajo la hipérbola. A veces también se refiere al logaritmo neperiano, a pesar de que el significado original de este término es ligeramente diferente.
Definición
Formalmente, la función ln(x) se define para valores reales positivos, como el área bajo la gráfica de 1/t entre 1 y x. Esta área corresponde a una integral:
La función logaritmo natural ln:R+→R se define como:
Mediante esta definición es inmediato comprobar que esta función cumple la propiedad fundamental de todo logaritmo:
 ,
,
Demostración En efecto, el logaritmo del producto de dos números positivos es: Podemos entonces descomponer la integral en dos tramos:
y realizar el cambio de variable s=t/x en la segunda integral:
El número para el cual esta función vale 1 resulta ser el número e. Por lo tanto, ln es el logaritmo con base e, o sea, la función inversa de ex.
Véase también
Referencias
- ↑ a b O'Connor, John J.; Robertson, Edmund F. (2001-09), «The number e» (en inglés), MacTutor History of Mathematics archive, Universidad de Saint Andrews, http://www-history.mcs.st-andrews.ac.uk/HistTopics/e.html, consultado el 02/02/2009
- ↑ Pietro Mengoli y Nicholas Mercator le dieron esta denominación por razones independientes del cálculo. Véase Ballew, Pat. «Math Words, and Some Other Words, of Interest». Consultado el 08-04-2011. y la anterior referencia de MacTutor (2001).
- ↑ Cajori, Florian (1991). A History of Mathematics, 5th ed. AMS Bookstore. pp. 152. ISBN 0821821024. http://books.google.com/?id=mGJRjIC9fZgC&dq=%22Cajori%22+%22A+History+of+Mathematics%22+.
- ↑ Flashman, Martin. «Estimating Integrals using Polynomials». Consultado el 23-03-2008.
Bibliografía
- "Cálculus" (Volumen I). Tom M. Apostol. Segunda edición, 1991. Editorial Reverté, S.A. ISBN 84-291-5002-1
- Este artículo fue creado a partir de la traducción del artículo Natural logarithm de la Wikipedia en inglés, bajo licencia Creative Commons Atribución Compartir Igual 3.0 y GFDL.
Enlaces externos
- Weisstein, Eric W. «Natural Logarithm» (en inglés). MathWorld. Wolfram Research.
Categoría:- Logaritmos
Wikimedia foundation. 2010.