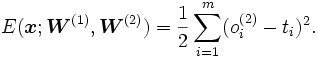- Propagación hacia atrás
-
Propagación hacia atrás
La propagación hacia atrás de errores o retropropagación (del inglés backpropagation) es un algoritmo de aprendizaje supervisado que se usa para entrenar redes neuronales artificiales. El algoritmo consiste en minimizar un error (comúnmente cuadrático) por medio de gradiente descendiente, por lo que la parte esencial del algoritmo es cálculo de las derivadas parciales de dicho error con respecto a los parámetros de la red neuronal.
Contenido
Minimización del Error
Los algoritmos en Aprendizaje Automático pueden ser clasificados en dos categorías: supervisados y no supervisados. Los algoritmos en aprendizaje supervisado son usados para construir "modelos" que generalmente predicen un ciertos valores deseados. Para ello, los algoritmos supervisados requieren que se especifiquen los valores de salida (output) u objetivo (target) que se asocian a ciertos valores de entrada (input). Ejemplos de objetivos pueden ser valores que indican éxito/fallo, venta/no-venta, pérdida/ganancia, o bien ciertos atributos multi-clase como cierta gama de colores o las letras del alfabeto. El conocer los valores de salida deseados permite determinar la calidad de la aproximación del modelo obtenido por el algoritmo.
La especificación de los valores entrada/salida se realiza con un conjunto consistente en pares de vectores con entradas reales de la forma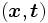 , conocido como conjunto de entrenamiento o conjunto de ejemplos. Los algoritmos de aprendizaje generalmente calculan los parámetros
, conocido como conjunto de entrenamiento o conjunto de ejemplos. Los algoritmos de aprendizaje generalmente calculan los parámetros  de una función
de una función  que permiten aproximar los valores de salida en el conjunto de entrenamiento.
que permiten aproximar los valores de salida en el conjunto de entrenamiento.
Si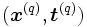 ,
, 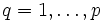 , son los elementos del conjunto de entrenamiento, la calidad de la aproximación en el ejemplo q se puede medir a través del error cuadrático:
, son los elementos del conjunto de entrenamiento, la calidad de la aproximación en el ejemplo q se puede medir a través del error cuadrático: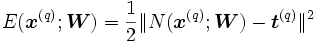 ,
,donde
 es la norma euclidiana.
es la norma euclidiana.El error total es la suma de los errores de los ejemplos:
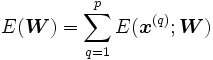 .
.
Un método general para minimizar el error es el actualizar los parámeros de manera iterativa. El valor nuevo de los parámetros se calcula al sumar un incremento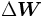 al valor actual:
al valor actual: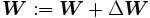
El algoritmo se detiene cuando
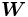 converge o bien cuado el error alcanza un mínimo valor deseado.
converge o bien cuado el error alcanza un mínimo valor deseado.Si la función
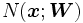 usada para aproximar los valores de salida es diferenciable respecto a los parámetros
usada para aproximar los valores de salida es diferenciable respecto a los parámetros 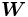 , podemos usar como algoritmo de aprendijaze el método de gradiende descendiente. En este caso, el incremento de los parámetros se expresa como
, podemos usar como algoritmo de aprendijaze el método de gradiende descendiente. En este caso, el incremento de los parámetros se expresa como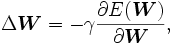
donde 0 < γ < 1 es un parámetro conocido como factor de aprendizaje.
Antes de continuar introduciremos un poco de notación. Definimos como el vector extendido del vector
como el vector extendido del vector 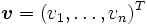 . El par
. El par 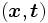 representará a un elemento del conjunto de entrenamiento y una relación de entrada-salida, a menos que se indique otra cosa.
representará a un elemento del conjunto de entrenamiento y una relación de entrada-salida, a menos que se indique otra cosa.Red Neuronal con una Capa Oculta
La función la usaremos para aproximar los valores de salida de una red neuronal artificial con una capa oculta. La red está constituida por una capa de entrada (input layer), una capa oculta (hidden layer) y una capa de salida (output layer), tal como se ilustra con la siguiente figura:
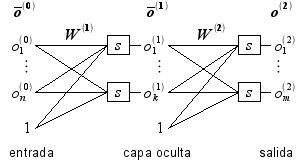
Los elementos que constituyen a la red neuronal son los siguientes:
- s es una función de valores reales, conocida como la función de transferencia.
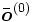 es la capa de entrada, considerado como el vector extendido del ejemplo
es la capa de entrada, considerado como el vector extendido del ejemplo 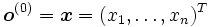 .
.
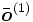 es la capa oculta, el vector extendido de
es la capa oculta, el vector extendido de 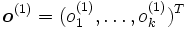 .
.
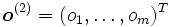 es la capa de salida, considerado como el vector que aproxima al valor deseado
es la capa de salida, considerado como el vector que aproxima al valor deseado 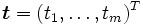 .
.
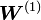 es una matriz de tamaño
es una matriz de tamaño 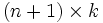 cuyos valores
cuyos valores 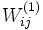 son los pesos de la conexión entre las unidades
son los pesos de la conexión entre las unidades 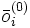 y
y 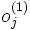 .
.
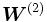 es una matriz de tamaño
es una matriz de tamaño 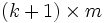 cuyos valores
cuyos valores 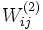 son los pesos de la conexión entre las unidades
son los pesos de la conexión entre las unidades 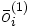 y
y 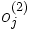 .
.
De estos elementos, únicamente las matrices
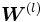 son consideradas como los parámetros de la red, ya que los valores
son consideradas como los parámetros de la red, ya que los valores 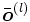 son el resultado de cálculos que dependen de las matrices de pesos, del valor de entrada
son el resultado de cálculos que dependen de las matrices de pesos, del valor de entrada 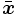 y de la función de transferencia s.
y de la función de transferencia s.
La función de transferencia s que consideraremos en nuestro algoritmo es conocida como función sigmoidal, y esta definida como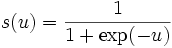
esta función además de ser diferenciable, tiene la particularidad de que su derivada se puede expresar en términos de sí misma:
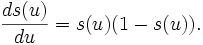
esto nos servirá para simplificar los cálculos en el algoritmo de aprendizaje aquí descrito.
Descripción del Algoritmo
A grandes rasgos:
- Calcular la salida de la red
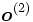 a partir de uno de los conjuntos de valores de prueba x.
a partir de uno de los conjuntos de valores de prueba x. - Comparar con la salida correcta t y calcular el error según la fórmula:
- Calcular las derivadas parciales del error con respecto a los pesos
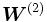 que unen la capa oculta con la de salida.
que unen la capa oculta con la de salida. - Calcular las derivadas parciales del error con respecto a los pesos
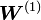 que unen la capa de entrada con la oculta.
que unen la capa de entrada con la oculta. - Ajustar los pesos de cada neurona para reducir el error.
- Repetir el proceso varias veces por cada par de entradas-salidas de prueba.
Cálculo de la Salída de la Red
Cálculo de las Derivadas Parciales
Ajuste de los Pesos
Entrenamiento On-Line y Off-Line
Enlaces externos
Referencias
- D. Michie, D.J. Spiegelhalter, C.C. Taylor (eds). Machine Learning, Neural and Statistical Classification, 1994. [1]
- R. Rojas. Neural Networks: A Systematic Introduction, Springer, 1996.ISBN 3-540-60505-3.
Categoría: Redes neuronales artificiales
Wikimedia foundation. 2010.