- Teorema de los tres momentos
-
El teorema de los tres momentos o teorema de Clapeyron es una relación deducida de la teoría de flexión de vigas y usada en en análisis estructural para resolver ciertos problemas de flexión hiperestática, fue demostrado por Émile Clapeyron a principios del siglo XIX.
Contenido
Enunciado
Dada una viga continua de material elástico lineal sobre varios apoyos simples, los momentos flectores en tres apoyos consecutivos satisfacen la relación:[1]
(1)

Donde
 , momento flector en el apoyo central, apoyo k-ésimo.
, momento flector en el apoyo central, apoyo k-ésimo. , momento flector en el apoyo a la izquierda, apoyo (k-1)-ésimo.
, momento flector en el apoyo a la izquierda, apoyo (k-1)-ésimo. , momento flector en el apoyo a la derecha, apoyo (k+1)-ésimo.
, momento flector en el apoyo a la derecha, apoyo (k+1)-ésimo. longitud del tramo de viga entre el apoyo (k-1)-ésimo y el apoyo k-ésimo
longitud del tramo de viga entre el apoyo (k-1)-ésimo y el apoyo k-ésimo longitud del tramo de viga entre el apoyok-ésimo y el apoyo (k+1)-ésimo.
longitud del tramo de viga entre el apoyok-ésimo y el apoyo (k+1)-ésimo. , área de los momentos flectores isostáticos en los tramos
, área de los momentos flectores isostáticos en los tramos  y
y  :
:
(2)
 son las distancias a los centros de gravedad de los diagramas de momentos flectores por la derecha y por la izquierda, el producto de estos por las áreas respectivas se puede calcular como:
son las distancias a los centros de gravedad de los diagramas de momentos flectores por la derecha y por la izquierda, el producto de estos por las áreas respectivas se puede calcular como:
(3)
Casos particulares
Carga continua y uniforme
Una fórmula frecuentemente empleada para tableros de puentos, viga y otros elementos con una carga uniforme es un caso particular del teorema de los tres momentos:

Cálculo de áreas y distancias
Las fórmulas integrales () y () no resultan cómodas en el caso general, sin embargo, para los casos má frecuentes de carga es posible calcular el área del diagarama de momentos isostáticos de cada tramo, y los centros de gravedad de estas áreas. Para un tramo de longitud L las magnitudes anteriores son:
-
Fórmulas para el área y los centros de gravedad Tipo de carga 




Uniforme
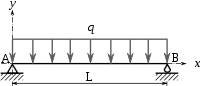


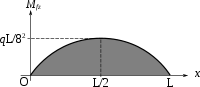



Puntual
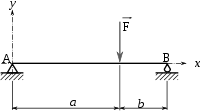

___
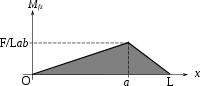



Triangular


![\frac{qL^2}{6}\left[\frac{x}{L}-\frac{x^3}{L^3}\right]](1/a51c97b39ef65b37a876b753808584d5.png)
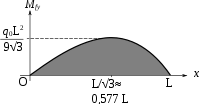



Potencial 
___ 


Uniforme inicial


___ 


Uniforme centrada
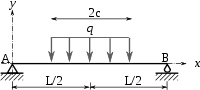

___ 


Senoidal 




Triangular centrada
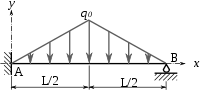

___ 


Teorema de los dos momentos
El teorema de los dos momentos es similar pero relaciona el momento flector en dos apoyos consecutivos pero requiere que uno de ellos sea un empotramiento. Si se tiene un empotramiento a la derecha y otro apoyo simple a la izquierda el teorema de los dos momentos establece que la relación entre ambos es:
(4a)

Expresión que puede obtenerse como caso límite del teorema de los tres momentos anterior haciendo
 y
y  . Si el empotramiento está en el apoyo de la izquierda:
. Si el empotramiento está en el apoyo de la izquierda:(4b)

Que también se obtiene de la expresión de los tres momentos haciendo
 y
y 
Cálculo de reacciones
Una vez determinados los momentos hiperestáticos con ayuda del teorema de los tres momentos el cálculo de reacciones verticales en cada uno de los apoyos se puede hacer fácilmente con ayuda de la siguiente fórmula:
(5)

Donde alguno de los términos anteriores debe tomarse igual a cero en el caso de los apoyos extremos por ser inexistente. Y donde:
 , es la reacción isostática en el apoyo de la izquierda del k-ésimo vano,
, es la reacción isostática en el apoyo de la izquierda del k-ésimo vano, , es la reacción isostática en el apoyo de la derecha del k-ésimo vano.
, es la reacción isostática en el apoyo de la derecha del k-ésimo vano.
Obviamente:

Ejemplos
Carga continua en dos vanos
- Viga continua con carga uniforme en toda su longitud, siendo las dos longitudes iguales, en este caso, reflejado en la figura de la derecha el teorema de los tres momentos lleva a:

Teniendo en cuenta que en este caso
 por ser los extremos de la viga articulados, usando la fórmula de cálculo del áreas y distancias conveniente (
por ser los extremos de la viga articulados, usando la fórmula de cálculo del áreas y distancias conveniente ( ) y susbstituyendo en la ecuación anterior se tiene que:
) y susbstituyendo en la ecuación anterior se tiene que:
y el diagrma de momentos flectores es como el de la figura de la derecha, y viene dado por:

El máximo momento flector positivo se obtiene buscando los puntos para los cuales la derivada de la función anterior se anula
 y
y  donde:
donde:
Las reacciones en los apoyos pueden calcularse fácilmente mediante las ecuaciones ():

Carga puntual en un vano
- Viga continua con carga puntual en el primer vano, siendo las dos longitudes iguales, en este caso, reflejado en la figura de la derecha el teorema de los tres momentos lleva a:

Teniendo en cuenta que en este caso
 por ser los extremos de la viga articulados, usando la fórmula de cálculo del áreas y distancias conveniente (
por ser los extremos de la viga articulados, usando la fórmula de cálculo del áreas y distancias conveniente ( ) y susbstituyendo en la ecuación anterior se tiene que:
) y susbstituyendo en la ecuación anterior se tiene que:
El momento flector máximo se da en el primer vano y puede ser calculado como:

y el diagrma de momentos flectores es como el de la figura de la derecha. Las reacciones en los apoyos calculadas mediante las ecuaciones de ():

Referencias
Bibliografía
- Ortiz Berrocal, L., Resistencia de materiales, McGraw-Hill, 2002, ISBN 84-481-3353-6.
Categorías:- Ingeniería mecánica
- Teoremas de resistencia de materiales
- Análisis estructural
Wikimedia foundation. 2010.








