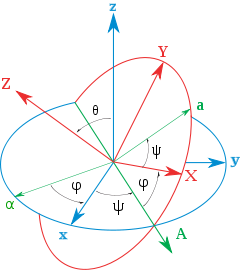
- Teorema de rotación de Euler
-
En geometría el Teorema de la rotación de Euler dice que, en un espacio tridimensional, cualquier movimiento de un sólido rígido que mantenga un punto constante, también debe dejar constante un eje completo. Esto también quiere decir que cualquier composición de rotaciones sobre un sólido rígido con ejes arbitrarios es equivalente a una sola rotación sobre un nuevo eje, llamado Polo de Euler. Al ser la combinación de rotaciones otra rotación, el conjunto de las operaciones de rotación tiene una estructura algebraica conocida como grupo. En concreto al grupo de rotaciones se le conoce como "grupo especial ortogonal de dimensión 3" o SO(3)
El teorema toma su nombre de Leonhard Euler, que lo demostró en 1775 con un argumento geométrico. La extensión de este concepto a la cinemática da el concepto de Eje instantáneo de rotación.
En términos de álgebra lineal, esto también quiere decir que el producto de dos matrices de rotación es también una matriz de rotación y que todas ellas tienen un único autovalor real que debe ser la unidad.
Teorema de Rotación de Euler(1776)
Euler enuncia su teorema de la siguiente forma:[1]
Theorema. Quomodocunque sphaera circa centrum suum conuertatur, semper assignari potest diameter, cuius directio in situ translato conueniat cum situ initiali.
que en traducción libre sería:
- Rotando una esfera de forma arbitraria alrededor de su centro, siempre es posible encontrar un diametro cuya posición tras la rotación es igual que la inicial
Para probar esto Euler primero toma un círculo máximo de la esfera fija y el círculo máximo correspondiente tras la rotación en la esfera rotada. Estos dos círculos se intersecan en dos puntos opuestos. Escogemos uno cualquiera A. Este punto está en el círculo inicial luego es transportado a otro punto a del segundo círculo. Pero también, A está en el círculo transportado, y por tanto corresponde a un punto α en el círculo inicial. En este punto, nótese que el arco aA debe ser igual al arco Aα.
Ahora Euler necesita un punto O en la superficie de la esfera situado de forma simétrica respecto de a y A. Si tal punto existe debe cumplir:
- Las distancias OA y Oa son iguales; los arcos Oa y OA también.
- Los arcos OA y Oa deben estar igualmente inclinados hacia los círculos y los arcos OAa y OAα deben ser iguales.
Euler define dos planos:
- El de simetría del ángulo αAa (que pasa por el centro C de la esfera), y
- El de simetría del arco Aa (que también pasa por C).
Proposición. Estos dos planos se intersecan en un diámetro de la esfera, el cual permanece fijo tras el movimiento.
Dem. Los planos se intersecan en un diámetro porque ambos pasan por el centro de la esfera. Sea O cualquiera de los puntos (hay dos) de corte del diámetro con la superficie de la esfera. Como αA se mueve a Aa y los triángulos tienen los mismos ángulos, el triangulo OαA se convierte en el triangulo OAa. Por tanto O debe permanecer fijo tras el movimiento. Lo mismo para el centro de la esfera y el punto antípoda de O.
Demostración algebraica
Una demostración matricial es posible teniendo en cuenta que una rotación se representa por una matriz ortogonal, es decir una tal que:
donde E es la identidad y T indica la traspuesta. Una matriz ortogonal tiene determinante ±1, siendo el +1 el caracteristico de las de rotación.
La matriz de rotación R tiene al menos un autovector n con autovalor λ = 1.
tenemos
luego λ = 1 es raíz de la ecuación
Habrá al menos un vector n, para el que
La línea dada por el espacio de todos los autovectores del autovalor 1 es el eje de Euler.
Notes
- ↑ Novi Commentarii academiae scientiarum Petropolitanae 20, 1776, pp. 189-207 (E478)
Categorías:- Teoremas de geometría
- Simetría euclidiana
Wikimedia foundation. 2010.