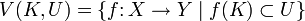- Base (topología)
-
Base (topología)
En matemáticas, una base β de un espacio topológico X con topología T, es una colección de abiertos de T que verifica que todo abierto de la topología T puede expresarse como unión de los elementos de β.
Decimos que la base genera la topología T y a los elementos de β les llamamos abiertos básicos. Las bases son de gran utilidad, pues muchas propiedades de las topologías pueden reducirse a afirmaciones sobre una base que genere dicha topología.
Una familia arbitraria de subconjuntos no formará a priori una base de ninguna topología, para hacerlo deberá reunir una serie de requisitos.
Existe un modo alternativo de generar una topología a partir de una familia arbitraria de subconjuntos, usando intersecciones finitas además de las uniones arbitrarias. En ese caso, la familia de subconjuntos recibe el nombre de subbase.
Contenido
Definición alternativa de base
Decimos que β es base de la topología T si y sólo si para todo punto p contenido en un abierto U existe un elemento
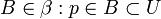 .
.Requisitos para que una familia de subconjuntos forme una base
Ya comentamos que una familia arbitraria de subconjuntos no formará una base. Será interesante disponer de un criterio para decidir si la forman o no.
Una familia β no vacía de subconjuntos de X formará la base de alguna topología si se cumple:
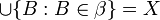 .
.- La intersección
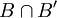 es unión de elementos de β.
es unión de elementos de β.
Subbase
En topología, una subbase para un espacio topológicio X con topología T, es una subcoleción B de T la cual genera a T, en el sentido que T es la topología más pequeña que contiene a B. Una definición levemente diferente es usada por algunos autores y existen otras formulaciones equivalentes, muy utiles, de la definición; estas son discutidas a continuación.
Definición
Sea X un espacio topológico con topología T. Una subbase de T es usualmente definida como una subcolección B de T que satisface una de las dos siguientes condiciones equivalentes:
- La subbcolección B genera la topología T. Esto significa que T es la topología mas pequeña que contiene a B: cualquier topología U en X que contiene a B también debe contener a T.
- La colección de conjuntos abiertos construida con X y todas la intersecciones finitas de los elementos de B forman una base para T. Esto significa que todo intervalo abierto propio no vacio en T puede ser escrito como una unión de intersecciones finitas de elementos de B.
Explicitamente, dado un punto x en un conjunto abierto propio U (vecindad de x) existen varios conjuntos finitos S1, …, Sn de B, tales que la intersección de estos conjutos contiene a x y esta contenuda en U.
(Note que si usamos la definición de intersección no vacia, entonces no es necesario incluir X en la segunda definición.)
Para alguna subcolleción S del conjunto de partes P(X), existe una única topología que tiene a S como una subbase. En particular, la intesección de todas las topologías en X que contiene a S, satisface esta condición. En general, no siempre existe una única subbase para una topología dada.
Por lo tanto, podemos comenzar con la topología fija y encontrar subbases para dicha topología, y podemos también comenzar con una subcolección arbitraria del conjunto de partes P(X) y formar la topología generada por esa subcolección. Podemos libremente usar cualquiera de las definiciones equivalenetes dadas anteriormente; ciertamente en muchos casos, una de las dos condiciones es más útil que la otra.
Definición alternativa
Algunas veces, una definición levemente diferente de subbase es dada, la cual requiere que la subbase B recubra a X. En este caso, X es un conjuto abierto en la topología generada poruqe es la unión de todos los {Bi} mientras Bi varia sobre B. Esto significa, que no pueden existir confusiones referentes al uso de la intersección no vacia, en la definición.
Sin embargo, con esta definición, las dos definiciones anteriores, no siempre son equivalentes. En otras palabras, existen espacios X con topología T, tales que existe una subcolección B de T, tal que T es la topología mas pequeña que contiene a B, donde B no cubre a X todavia. En la practica, es una rara ocurrecia; una subbase de un espacio que satisface el T1 debe ser una cobertura de éste espacio.
Ejemplos
La topología usual en los números reales R tiene una subbase formada por todos los intervalos abiertos semi-infinitos bien sea de la forma (−∞,a) or (b,∞) donde a y b son números reales. Juntos generan la topología usual desde las intersecciones
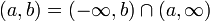 para a < b genera la topología usual. Una segunda subbase es formada, tomando la subfamilia donde a y b son racionales. La segunda subbase genera la topología usual también, desde los intervalos abiertos (a,b) con a, b racionales, son una base para la topología ususal Euclidiana.
para a < b genera la topología usual. Una segunda subbase es formada, tomando la subfamilia donde a y b son racionales. La segunda subbase genera la topología usual también, desde los intervalos abiertos (a,b) con a, b racionales, son una base para la topología ususal Euclidiana.La subbase formada por todos los intervalos abiertos semi-infinitos de la forma (−∞,a), donde a es un número real, que no genera la topología usual. La topología resultante no satisface el axioma T1 de separación, desde todos los conjuntos abiertos que tiene una intersección no vacia.
La topología inicial definida por la familia de funciones fi : X → Yi, donde cada Yi tiene una topología, es la topología más gruesa en X, tal que cada fi es continua; ya que la continuidad puede ser definida por las imagenes inversas de los conjuntos abiertos; ésto significa que la topología más debil en X es dada tomando todas las fi−1(Ui), donde Ui varia en todo el conjunto abieto de Yi, como una subbase.
Dos casos especiales muy importantes de la topología inicial son la topología del producto, donde la familia de funciones es el conjunto de proyecciones desde el producto a cada factor, y el subespacio topologíco, donde la familia consta de solo una función, la función de inclusión.
La topología compacta abierta, en el espacio de funciones continuas de X a Y tiene por una subbase el conjunto de funciones
donde K es un espacio compacto y U es abierto en Y.
Referencias
- Dugundji, J. Topology, McGraw-Hill Companies, 1966. ISBN 0-697-06889-7. (Capítulo III)
- Stephen Willard, General Topology, (1970) Addison-Wesley Publishing Company, Reading Massachusetts.
Categoría: Topología general
Wikimedia foundation. 2010.