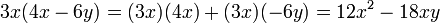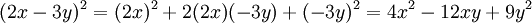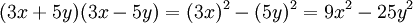Binomio

Binomio

Saltar a navegación, búsqueda

En álgebra, un binomio es una expresión algebraica con dos términos. Estrictamente hablando se refiere a un polinomio formado por la suma de dos monomios, aunque se usa de forma más fácil para indicar cualquier expresión que consta de una suma o resta de dos términos.

Bajo la definición estricta, son binomios las expresiones:

$x^2-3y, \qquad 5a+\sqrt{3}$

mientras que no lo son expresiones tales como:

$\cos(x)-\tan(x),\qquad e^{x}-1, \qquad x^2-\sqrt{x+1}$

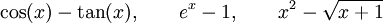
puesto que alguno de sus términos no es un monomio, aunque en un contexto más informal podría llamarse binomio a cualquier expresión que involucre una suma o resta de dos expresiones. Así, es posible encontrar en un libro de álgebra un ejercicio en la sección de "binomios al cuadrado" que diga «Calcula el resultado de (cos(x)+sen(x))²».

Grado de un binomio

Para hallar el grado de un binomio :c, se calcula la suma de exponentes en cada término. La mayor suma es el grado.

Así, en el binomio 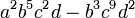$a^2b^5c^2d-b^3c^9d^2\,$ el primer monomio tiene grado 2+5+2+1 = 10, mientras que el grado del segundo es 3+9+2 = 14, por lo que el binomio tiene grado 14.

El binomio 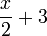$\frac{x}{2}+3\,$ tiene grado 1, puesto que el grado de x = x¹ es 1, mientras que el grado del número 3 es cero.

Productos notables

Artículo principal: Productos notables

Representación gráfica de la regla de factor común

Existen ciertas fórmulas que permiten multiplicar ciertos polinomios de forma directa (sin realizar la multiplicación completa). Tales fórmulas se denominan productos notables y muchas de ellas se refieren a operaciones con binomios. Estos productos suelen ser estudiados con detalle en los primeros cursos de álgebra.

Factor común

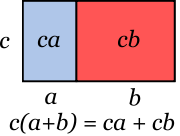
El resultado de multiplicar un binomio a+b con un término c se obtiene aplicando la propiedad distributiva:

$c (a + b) = c a + c b \,$

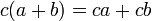
o realizando la operación:

$\begin{array}{rrr} & a & +b \\ \times & & c \\ \hline & ca & +cb \end{array}$

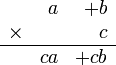
Esta operación tiene una interpretación geométrica ilustrada en la figura. El área del rectángulo es c(a+b) (el producto de la base por la altura), pero también puede obtenerse como la suma de las dos áreas coloreadas (ca y cb).

Ejemplo:

$3x (4x-6y) = (3x)(4x) + (3x)(-6y) = 12x^2 - 18xy \,$

Cuadrado de binomio

Visualización de la fórmula para binomio al cuadrado

Elevando un binomio al cuadrado es decir, se multiplica por sí mismo:

$(a + b)^2 = (a + b) \times (a + b) \,$

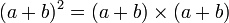
que se puede multiplicar así:

$\begin{array}{rrr} & a & +b \\ \times & a & +b \\ \hline & +ab & +b^2 \\ a^2 & +ab & \\ \hline a^2 & +2ab & +b^2 \end{array}$

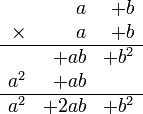
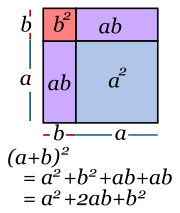
Por lo que se puede expresar una regla para el cálculo directo: se suman los cuadrados cada término con el doble producto de los mismos. Es decir:

$(a + b)^2 = a^2 + 2 a b + b^2 \,$

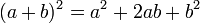
Un trinomio de la forma 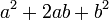$a^2 + 2 a b + b^2 \,$, se conoce como trinomio cuadrado perfecto;

Cuando el segundo término es negativo:

$(a - b)^2 = (a - b) \times (a - b) \,$

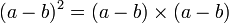
la forma con la que se obtiene es:

$\begin{array}{rrr} & a & -b \\ \times & a & -b \\ \hline & -ab & +b^2 \\ a^2 & -ab & \\ \hline a^2 & -2ab & +b^2 \end{array}$

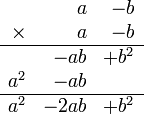
esto es:

$(a - b)^2 = a^2 - 2 a b + b^2 \,$

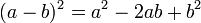
Ejemplo:

$(2x - 3y)^2 = (2x)^2 + 2(2x)(-3y)+ (-3y)^2 = 4x^2 -12xy +9y^2 \,$

Suma por Diferencia

El resultado de la operación:

$(a + b)(a - b) \,$

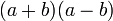
es:

$\begin{array}{rrr} & a & +b \\ \times & a & -b \\ \hline & -ab & -b^2 \\ a^2 & +ab & \\ \hline a^2 & & -b^2 \end{array}$

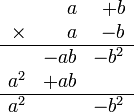
Que se suele decir: suma por diferencia, diferencia de cuadrados:

$(a + b)(a - b) = a^2 - b^2 \,$

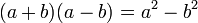
Ejemplo:

$(3x+5y)(3x-5y) = (3x)^2 - (5y)^2 = 9x^2 - 25y^2 \,$

Producto de binomios conjugados

Dos binomios que sólo se diferencian en el signo de la operación se denominan binomios conjugados. Para multiplicar binomios conjugados, basta elevar los monomios al cuadrado y restarlos, obteniendo una diferencia de cuadrados

$a^2 - b^2 = (a + b)(a - b) \,$

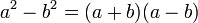
Ejemplo:

$(3x+5y)(3x-5y) = (3x)^2 - (5y)^2 = 9x^2 - 25y^2 \,$

Otros usos del término

De forma coloquial se emplea binomio para denotar un par de conceptos o personas relacionadas. Así, se puede hablar de el binomio de Batman y Robin (pareja) o el binomio cliente/servidor (en informática).

Véase también

• Teorema del binomio
• Monomio
• Trinomio
• Polinomio

Referencias

Wentworth, George; y Smith, David Eugene (1917). Ginn & Co. (ed.). Elementos de Algebra, 2a edición, pp. 456. ISBN.

Enlaces externos

Wikcionario

• Wikcionario tiene definiciones para binomio.

Obtenido de "Binomio"