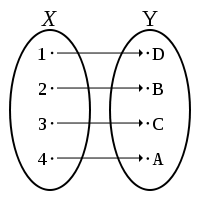
Función biyectiva

Ejemplo de función biyectiva.

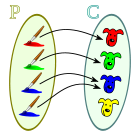
En matemática, una función $f \colon X \to Y \,$ es biyectiva si es al mismo tiempo inyectiva y sobreyectiva; es decir, si todos los elementos del conjunto de salida tienen una imagen distinta en el conjunto de llegada, y a cada elemento del conjunto de llegada le corresponde un elemento del conjunto de salida.

Formalmente,

$\forall y\in Y : \exists !\ x\in X,\ f(x) = y$

Una implicación directa de lo anterior, es que en una función biyectiva la cardinalidad del conjunto de salida o dominio, y el de llegada o codominio, son iguales. Esto también se puede ver en el ejemplo, donde |X|=|Y|=4.

Teorema

Si $f\,$ es una función biyectiva, entonces su función inversa $f^{-1}\,$ existe y también es biyectiva.

Ejemplo

La función:

$f(x) =6x + 9 \,$

es biyectiva.

Luego, su inversa:

$f^{-1}(y) = \frac{y - 9}{6} \,$

también lo es.^[1]

El siguiente diagrama se puede ver cuando la función es biyectiva:

Funciones	Inyectiva	No inyectiva
Sobreyectiva	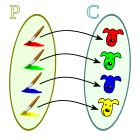Biyectiva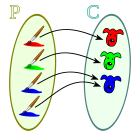
No sobreyectiva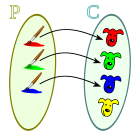

Véase también

• Función inyectiva
• Función sobreyectiva
• Correspondencia biunívoca

Referencias

1. ↑ Como consecuencia de la afirmación de que toda función biyectiva tiene una inversa también biyectiva, lo cual se puede intuir gráficamente, se deduce analíticamente que el Dominio de toda función biyectiva corresponde a la Imagen de su inversa, y viceversa.

Enlaces externos

• Weisstein, Eric W. «Bijection» (en inglés). MathWorld. Wolfram Research.