- Caída libre
-
Caída libre
En mecánica, la caída libre se refiere al movimiento de un cuerpo bajo la acción exclusiva de un campo gravitatorio. Aunque la definición excluya la acción de otras fuerzas, como la resistencia aerodinámica, frecuentemente se incluyen otras fuerzas que influyen en el movimiento de cuerpo cuando tiene lugar en el seno de un fluido (la atmósfera, un líquido,etc.).
Se refiere también a caída libre como una trayectoria geodésica en el espacio-tiempo de cuatro dimensiones de la Teoría de la Relatividad General.
Contenido
La caída libre como sistema de referencia
Un sistema de referencia ligado a un cuerpo en caída libre puede considerarse inercial o no inercial en función del marco teórico que esté utilizándose.
En la física clásica, la fuerza gravitatoria que se ejerce una masa es proporcional a la intensidad del campo gravitatorio en la posición espacial donde se encuentre dicha masa. La constante de proporcionalidad es precisamente el valor de la masa inercial del cuerpo, tal y como establece el principio de equivalencia. En la física relativista, la gravedad es el efecto que produce sobre las trayectorias de los cuerpos la curvatura del espacio-tiempo; en este caso, la gravedad no es una fuerza, sino una geodésica.
Por tanto, desde el punto de vista de la física clásica, un sistema de referencia en caída libre es un sistema acelerado por la fuerza de la gravedad y, como tal, es no inercial. Por el contrario, desde el punto de vista de la física relativista, el mismo sistema de referencia es inercial, pues aunque está acelerado en el espacio, no está acelerado en el espacio-tiempo. La diferencia radica en la propia definición de los conceptos geométricos y cinemáticos, que para cada marco teórico son completamente diferentes.
Aceleración en caída libre
 Caída' libre
Caída' libre
En la caida libre propiamente dicha, se desprecia la resistencia aerodinámaca que presenta el aire al movimiento del cuerpo o se analiza lo que pasaría en el vacío.
Cuando el cuerpo parte del reposo, el movimiento de caída libre es un movimiento rectilíneo uniformemente acelerado. La aceleración, debida sólo a la gravedad, es independiente de la masa del cuerpo; es decir, si dejamos caer una bala de cañón y una pluma, ambos cuerpos adquieren la misma aceleración,
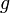 , que es la aceleración de la gravedad.
, que es la aceleración de la gravedad.Cuando la caída libre tiene lugar en el seno de un fluido (como el aire), hay que considerar la resistencia aerodinámica que actúa sobre el cuerpo. Aunque técnicamente la caída ya no es libre, desarrollaremos en adelante las ecuaciones incluyendo el término aerodinámico excepto en los casos en los que no proceda (p.e. espacio exterior).
Caída libre en campo aproximadamente constante
Por la segunda ley de Newton, la fuerza
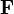 que actúa sobre un cuerpo es igual al producto de la masa
que actúa sobre un cuerpo es igual al producto de la masa 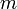 de éste por la aceleración que adquiere. En caída libre sólo intervienen el peso
de éste por la aceleración que adquiere. En caída libre sólo intervienen el peso 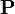 (vertical, hacia abajo) y el rozamiento aerodinámico
(vertical, hacia abajo) y el rozamiento aerodinámico 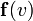 en la misma dirección y sentido opuesto a la velocidad. La ecuación de movimiento es por tanto:
en la misma dirección y sentido opuesto a la velocidad. La ecuación de movimiento es por tanto: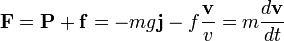
La aceleración de la gravedad lleva signo negativo porque tomamos el eje y hacia arriba.
Trayectoria en caída libre
Caída libre totalmente vertical
El movimiento del cuerpo en caída libre es vertical con velocidad creciente (aproximadamente movimiento uniformemente acelerado con aceleración g) (aproximadamente porque la aceleración aumenta cuando el objeto disminuye en altura, en la mayoría de los casos la variación es despreciable). La ecuación de movimiento se puede escribir en términos la altura y:
(1)
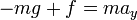
donde:
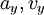 , son la aceleración y la velocidad verticales.
, son la aceleración y la velocidad verticales. , es la fuerza de rozamiento fluidodinámico (que aumenta con la velocidad).
, es la fuerza de rozamiento fluidodinámico (que aumenta con la velocidad).
- Si, en primera aproximación, se desprecia la fuerza de rozamiento, cosa que puede hacerse para caídas desde pequeñas alturas de cuerpos relativamente compactos, en las que se alcanzan velocidades moderadas, la solución de la ecuación diferencial () para las velocidades y la altura vienen dada por:
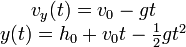
donde v0 es la velocidad inicial, para una caída desde el reposo v0 = 0 y h0 es la altura inicial de caída.
- Para grandes alturas u objetos de gran superficie (una pluma, un paracaídas) es necesario tener en cuenta la resistencia fluidodinámica que suele ser modelizada como una fuerza proporcional a la velocidad, siendo la constante de proporcionalidad el llamado rozamiento aerodinámico kw:
(2)
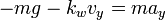
En este caso la variación con el tiempo de la velocidad y el espacio recorrido vienen dados por la solución de la ecuación diferencial ():
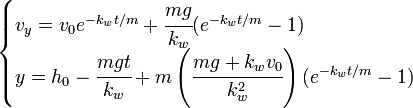
Nótese que en este caso existe una velocidad límite dada por el rozamiento aerodinámico y la masa del cuerpo que cae:
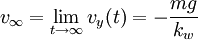
- Un análisis más cuidadoso de la fricción de un fluido revelaría que a grandes velocidades el flujo alrededor de un objeto no puede considerarse laminar, sino turbulento y se producen remolinos alrededor del objeto que cae de tal manera que la fuerza de fricción se vuelve proporcional al cuadrado de la velocidad:
(3)
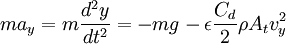
Donde:
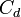 , es el coeficiente aerodinámico de resistencia al avance, que sólo depende de la forma del cuerpo.
, es el coeficiente aerodinámico de resistencia al avance, que sólo depende de la forma del cuerpo.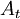 , es el área transversal a la dirección del movimiento.
, es el área transversal a la dirección del movimiento.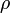 , es la densidad del fluido.
, es la densidad del fluido.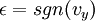 , es el signo de la velocidad.
, es el signo de la velocidad.
La velocidad límite puede calcularse fácilmente poniendo igual a cero la aceleración en la ecuación ():
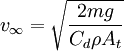
La solución analítica de la ecuación diferencial () depende del signo relativo de la fuerza de rozamiento y el peso por lo que la solución analítica es diferente para un cuerpo que sube hacia arriba o para uno que cae hacia abajo. La solución de velocidades para ambos casos es:
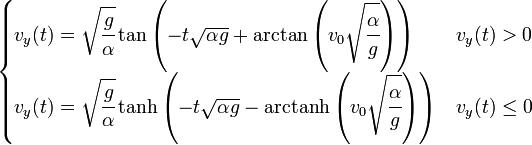
Donde:
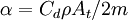 .
.Si se integran las ecuaciones anteriores para el caso de caída libre desde una altura h0 y velocidad inicial nula y para el caso de lanzamiento vertical desde una altura nula con una velocidad inicial v0 se obtienen los siguientes resultados para la altura del cuerpo:
Caída libre (v0 = 0 y y(0) = h0):
![y(t)=h_0-\cfrac{1}{{\alpha}}\ln\left[\cosh\left(-t\sqrt{{\alpha}{g}}\right) \right]](/pictures/eswiki/54/64407f2d5c666902f084e7350c123773.png)
El tiempo transcurrido en la caída desde la altura y = h0 hasta la altura y = 0 puede obtenerse al reordenar la ecuación anterior:
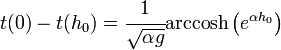
Lanzamiento vertical (v0 = v0 y y(0) = 0):
![y(t)=\cfrac{1}{{\alpha}}\ln\left[\cfrac{\cos\left[-t\sqrt{{\alpha}{g}}+\arctan\left(v_0\sqrt{\cfrac{\alpha}{g}}\right)\right]}{\cos\left[\mbox{arctan}\left(v_0\sqrt{\cfrac{\alpha}{g}}\right)\right]} \right]](/pictures/eswiki/49/162a803c65007695a5634885c3c8cce0.png)
Si la altura h0 es aquella en que la velocidad vertical se hace cero, entonces el tiempo transcurrido desde el lanzamiento hasta el instante en que se alcanza la altura h0 puede calcularse como:
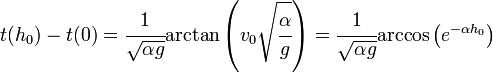
Se puede demostrar que el tiempo que tarda un cuerpo en caer desde una altura h0 hasta el suelo a través del aire es mayor que el que tarda el mismo cuerpo en alcanzar la alura máxima de h0 si es lanzado desde el suelo. Para ello basta con probar la desigualdad siguiente:
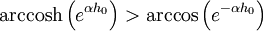
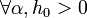
sabiendo que
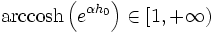 y que
y que ![\mbox{arccos}\left(e^{-{\alpha}h_0}\right)\in\left[0,\cfrac{\pi}{2}\right]](/pictures/eswiki/50/2a8f254b20cdbb409d09efc8c1990a48.png)
Caída libre parabólica y casi-parabólica
Cuando un cuerpo cae en caída libre pero no parte del reposo porque tiene una velocidad no nula, entonces la trayectoria de caída no es una recta sino una curva aproximadamente parabólica. La ecuación de la trayectoria en coordenadas cartesianas, donde x va a ser la distancia recorrida horizontalmente y y la altura sobre el nivel del suelo viene dada simplemente por:
(4)
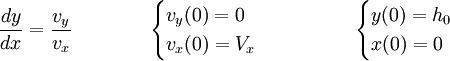
Donde la expresión de la velocidad vertical debe reescribirse en función de la coordanada x teniendo en cuenta que t = x/vx. Pueden distinguirse los siguientes casos:
- Para un cuerpo en caída libre sin rozamiento la curva trayectoria es exactamente una parábola dada por:
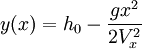
- Cuando se incluye el rozamiento aerodinámico la curva no es exactamente una parábola. Por ejemplo para una fuerza de rozamiento proporcional a la velocidad como en la () la trayectoria resulta ser:
![y(x) = h_0 - \delta \left[\frac{x}{\beta\delta}-\ln \left(1-\frac{x}{\beta\delta} \right) \right] \qquad \begin{cases} \delta = gm^2/k_w^2\\ \beta = V_xk_w/mg\end{cases}](/pictures/eswiki/50/2499cfce560492266eba090a5e021837.png)
Para una fuerza de rozamiento proporcional al cuadrado de la velocidad la integración de las ecuaciones del movimiento es más compleja, presuponiendo fuerzas de rozamiento independientes en dirección horizontal y vertical proporcionales al cuadrado del valor de la componente:
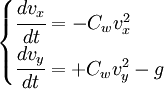
La trayectoria viene dada por:
![y(x) = h_0 - \delta \ln \left[\cosh \left( \frac{e^{x/\delta}-1}{\beta}\right) \right] \qquad \begin{cases} \delta = 1/C_w\\ \beta = \sqrt{g/(C_wV_x^2)} \end{cases}](/pictures/eswiki/51/3bf3fe9845c590f97bd6f85495e3efd4.png)
Las figuras adjuntas muestran la forma de las trayectorias para cinco valores diferentes del parámetro β para una misma altura de caída (medida en unidades de longitud δ).
 Rozamiento -kwv. Trayectorias casi parabólicas con rozamiento proporcional a la velocidad, para cinco valores diferentes de la velocidad horizontal β = 1,5, β = 2,5, β = 3,5 y β = 4,5, desde una altura h = 7δ
Rozamiento -kwv. Trayectorias casi parabólicas con rozamiento proporcional a la velocidad, para cinco valores diferentes de la velocidad horizontal β = 1,5, β = 2,5, β = 3,5 y β = 4,5, desde una altura h = 7δ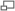
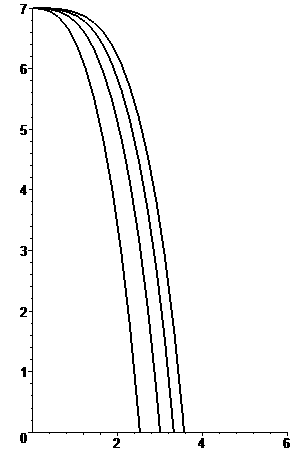 Rozamiento -Cwv2. Trayectorias casi parabólicas con rozamiento proporcional al cuadrado de la velocidad, para cinco valores diferentes de la velocidad horizontal β = 1,5, β = 2,5, β = 3,5 y β = 1,5, desde una altura h = 7δ
Rozamiento -Cwv2. Trayectorias casi parabólicas con rozamiento proporcional al cuadrado de la velocidad, para cinco valores diferentes de la velocidad horizontal β = 1,5, β = 2,5, β = 3,5 y β = 1,5, desde una altura h = 7δ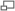
Caída libre desde grandes distancias: cónicas
La caída libre desde grandes alturas en un campo gravitatorio aproximadamente esférico, como es el caso de la Tierra requiere correcciones importantes ya que en ese caso ni la dirección ni la magnitud de la fuerza gravitatoria es constante. Concretamente para un campo gravitatorio newtoniano con simetría esférica la trayectoria es un arco elipse, cuando podemos ignorar el rozamiento con la atmósfera.
Véase también
Enlaces externos
Categorías: Cinemática | Gravedad
Wikimedia foundation. 2010.
