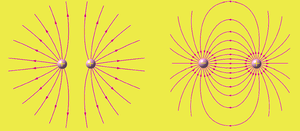
- Campo eléctrico
-
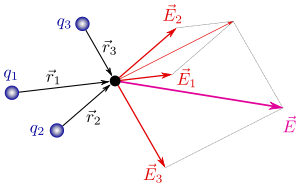 Campo eléctrico producido por un conjunto de cargas puntuales. Se muestra en rosa la suma vectorial de los campos de las cargas individuales;
Campo eléctrico producido por un conjunto de cargas puntuales. Se muestra en rosa la suma vectorial de los campos de las cargas individuales;
 .
.El campo eléctrico es un campo físico que es representado mediante un modelo que describe la interacción entre cuerpos y sistemas con propiedades de naturaleza eléctrica.[1] Matemáticamente se describe como un campo vectorial en el cual una carga eléctrica puntual de valor q sufre los efectos de una fuerza eléctrica
 dada por la siguiente ecuación:
dada por la siguiente ecuación:(1)

En los modelos relativistas actuales, el campo eléctrico se incorpora, junto con el campo magnético, en campo tensorial cuadridimensional, denominado campo electromagnético Fμν.[2]
Los campos eléctricos pueden tener su origen tanto en cargas eléctricas como en campos magnéticos variables. Las primeras descripciones de los fenómenos eléctricos, como la ley de Coulomb, sólo tenían en cuenta las cargas eléctricas, pero las investigaciones de Michael Faraday y los estudios posteriores de James Clerk Maxwell permitieron establecer las leyes completas en las que también se tiene en cuenta la variación del campo magnético.
Esta definición general indica que el campo no es directamente medible, sino que lo que es observable es su efecto sobre alguna carga colocada en su seno. La idea de campo eléctrico fue propuesta por Faraday al demostrar el principio de inducción electromagnética en el año 1832.
La unidad del campo eléctrico en el SI es Newton por Culombio (N/C), Voltio por metro (V/m) o, en unidades básicas, kg·m·s−3·A−1 y la ecuación dimensional es MLT-3I-1.
Contenido
Definición
El campo eléctrico es una perturbación que modifica el espacio que lo rodea, dicho campo puede provenir, por ejemplo, de una carga eléctrica puntual. Se considera un ente físico no visible, pero si medible, y se lo modeliza matemáticamente como el vector campo eléctrico, que se define como la relación entre la Fuerza Coulombiana que experimenta una carga testigo y el valor de la carga testigo (una carga testigo positiva). La definición más intuitiva del campo eléctrico se la puede dar mediante la ley de Coulomb. Esta ley, una vez generalizada, permite expresar el campo entre distribuciones de carga en reposo relativo. Sin embargo, para cargas en movimiento se requiere una definición más formal y completa, se requiere el uso de cuadrivectores y el principio de mínima acción. A continuación se describen ambas.
Definición mediante la ley de Coulomb
Campo eléctrico de una distribución lineal de carga. Una carga puntual P es sometida a una fuerza en direccion radial
 por una distribucion de carga λ en forma de diferencial de linea (dL), lo que produce un campo eléctrico
por una distribucion de carga λ en forma de diferencial de linea (dL), lo que produce un campo eléctrico  .
.Partiendo de la ley de Coulomb que expresa que la fuerza entre dos cargas en reposo relativo depende del cuadrado de la distancia, matemáticamente es igual a:[1]

Donde:
 es la permitividad eléctrica del vacío tiene que ver con el sistema internacional,
es la permitividad eléctrica del vacío tiene que ver con el sistema internacional, son las cargas que interactúan,
son las cargas que interactúan, es la distancia entre ambas cargas,
es la distancia entre ambas cargas, , es el vector de posición relativa de la carga 2 respecto a la carga 1.
, es el vector de posición relativa de la carga 2 respecto a la carga 1.
y
 es el unitario en la dirección
es el unitario en la dirección  . Nótese que en la fórmula se está usando
. Nótese que en la fórmula se está usando  , esta es la permitividad en el vacío. Para calcular la interacción en otro medio es necesario cambiar la permitividad de dicho medio. (
, esta es la permitividad en el vacío. Para calcular la interacción en otro medio es necesario cambiar la permitividad de dicho medio. ( )
)La ley anterior presuponía que la posición de una partícula en un instante dado, hace que su campo eléctrica afecte en el mismo instante a cualquier otra carga. Ese tipo de interacciónes en las que el efecto sobre el resto de partículas parece dependender sólo de la posición de la partícula causante sin importar la distancia entre las partículas se denomina en física acción a distancia. Si bien la noción de acción a distancia fue aceptada inicialmente por el propio Newton, experimentos más cuidados a lo largo del siglo XIX llevaron a desechar dicha noción como no-realista. En ese contexto se pensó que el campo eléctrico no sólo era un artificio matemático sino un ente físico que se propaga a una velocidad finita (la velocidad de la luz) hasta afectar a otras partículas. Esa idea conllevaba modificar la ley de Coulomb de acuerdo con los requerimientos de la teoría de la relatividad y dotar de entidad física al campo eléctrico.[1] Así, el campo eléctrico es una distorsión electromagnética que sufre el espacio debido a la presencia de una carga. Considerando esto se puede obtener una expresión del campo eléctrico cuando este sólo depende de la distancia entre las cargas:

Donde claramente se tiene que
 , la que es una de las definiciones más conocidas acerca del campo eléctrico.
, la que es una de las definiciones más conocidas acerca del campo eléctrico.Definición formal
La definición más formal de campo eléctrico, válida también para cargas moviéndose a velocidades cercanas a la de la luz, surge a partir de calcular la acción de una partícula cargada en movimiento a través de un campo electromagnético.[2] Este campo forma parte de un único campo electromagnético tensorial Fμν definido por un potencial cuadrivectorial de la forma:[1]
(1)

donde φ es el potencial escalar y
 es el potencial vectorial tridimensional. Así, de acuerdo al principio de mínima acción, se plantea para una partícula en movimiento en un espacio cuadridimensional:
es el potencial vectorial tridimensional. Así, de acuerdo al principio de mínima acción, se plantea para una partícula en movimiento en un espacio cuadridimensional:(2)

donde e es la carga de la partícula, m es su masa y c la velocidad de la luz. Reemplazando () en () y conociendo que dxi = uids, donde dxi es el diferencial de la posición definida dxi = (cdt,dx,dy,dz) y ui es la velocidad de la partícula, se obtiene:
(3)

El término dentro de la integral se conoce como el lagrangiano del sistema; derivando esta expresión con respecto a la velocidad se obtiene el momento de la partícula, y aplicando las ecuaciones de Euler-Lagrange se encuentra que la variación temporal de la cantidad de movimiento de la partícula es:
(4)

De donde se obtiene la fuerza total de la partícula. Los dos primeros términos son independientes de la velocidad de la partícula, mientras que el último depende de ella. Entonces a los dos primeros se les asocia el campo eléctrico y al tercero el campo magnético. Así se encuentra la definición más general para el campo eléctrico:[2]
(5)

La ecuación () brinda mucha información acerca del campo eléctrico. Por un lado, el primer término indica que un campo eléctrico es producido por la variación temporal de un potencial vectorial descrito como
 donde
donde  es el campo magnético; y por otro, el segundo representa la muy conocida descripción del campo como el gradiente de un potencial.[2]
es el campo magnético; y por otro, el segundo representa la muy conocida descripción del campo como el gradiente de un potencial.[2]Descripción del campo eléctrico
Matemáticamente un campo se lo describe mediante dos de sus propiedades, su divergencia y su rotacional. La ecuación que describe la divergencia del campo eléctrico se la conoce como ley de Gauss y la de su rotacional es la ley de Faraday.[1]
Ley de Gauss
Para conocer una de las propiedades del campo eléctrico se estudia que ocurre con el flujo de éste al atravesar una superficie. El flujo de un campo Φ se lo obtiene de la siguiente manera:
(8)

donde
 es el diferencial de área en dirección normal a la superficie. Aplicando la ecuación () en () y analizando el flujo a través de una superficie cerrada se encuentra que:
es el diferencial de área en dirección normal a la superficie. Aplicando la ecuación () en () y analizando el flujo a través de una superficie cerrada se encuentra que:(9)

donde Qenc es la carga encerrada en esa superficie. La ecuación () es conocida como la ley integral de Gauss y su forma derivada es:
(10)

donde ρ es la densidad volumétrica de carga. Esto indica que el campo eléctrico diverge hacia una distribución de carga; en otras palabras, que el campo eléctrico comienza en una carga y termina en otra.[1]
Esta idea puede ser visualizada mediante el concepto de líneas de campo. Si se tiene una carga en un punto, el campo eléctrico estaría dirigido hacia la otra carga.
Ley de Faraday
En 1801, Michael Faraday realizó una serie de experimentos que lo llevaron a determinar que los cambios temporales en el campo magnético inducen un campo eléctrico. Esto se conoce como la ley de Faraday. La fuerza electromotriz, definida como el rotacional a través de un diferencial de línea está determinado por:
(11)

donde el signo menos indica la Ley de Lenz y Φ es el flujo magnético en una superficie, determinada por:
(12)

reemplazando () en () se obtiene la ecuación integral de la ley de Faraday:
(13)

Aplicando el teorema de Stokes se encuentra la forma diferencial:
(14)

La ecuación () completa la descripción del campo eléctrico, indicando que la variación temporal del campo magnético induce un campo eléctrico.[1]
Expresiones del campo eléctrico
Campo electrostático (cargas en reposo)
Un caso especial del campo eléctrico es el denominado electrostático. Un campo electrostático no depende del tiempo, es decir es estacionario. Para este tipo de campos la Ley de Gauss todavía tiene validez debido a que esta no tiene ninguna consideración temporal, sin embargo, la Ley de Faraday debe ser modificada. Si el campo es estacionario, la parte derecha de la ecuación () y () no tiene sentido, por lo que se anula:
(15)

Esta ecuación junto con () definen un campo electrostático. Además, por el cálculo diferencial, se sabe que un campo cuyo rotacional es cero puede ser descrito mediante el gradiente de una función escalar V, conocida como potencial eléctrico:
(16)

La importancia de () radica en que debido a que el rotacional del campo eléctrico es cero, se puede aplicar el principio de superposición a este tipo de campos. Para varias cargas, se define el campo eléctrico como la suma vectorial de sus campos individuales:
(17)

entonces
(18)

Líneas de campo
Un campo eléctrico estático puede ser representado geométricamente con líneas tales que en cada punto el campo vectorial sea tangente a dichas líneas, a estas líneas se las conoce como "líneas de campo". Matemáticamente las líneas de campo son las curvas integrales del campo vectorial. Las líneas de campo se utilizan para crear una representación gráfica del campo, y pueden ser tantas como sea necesario visualizar.
Las líneas de campo son líneas perpendiculares a la superficie del cuerpo, de manera que su tangente geométrica en un punto coincide con la dirección del campo en ese punto. Esto es una consecuencia directa de la ley de Gauss, es decir encontramos que la mayor variación direccional en el campo se dirige perpendicularmente a la carga. Al unir los puntos en los que el campo eléctrico es de igual magnitud, se obtiene lo que se conoce como superficies equipotenciales, son aquellas donde el potencial tiene el mismo valor numérico. En el caso estático al ser el campo eléctrico un campo irrotacional las líneas de campo nunca serán cerradas (cosa que sí puede suceder en el caso dinámico, donde el rotacional del campo eléctrico es igual a la variación temporal del campo magnético cambiada de signo, por tanto una línea de campo eléctrico cerrado requiere un campo magnético variable, cosa imposible en el caso estático).
En el caso dinámico pueden definirse igualmente las líneas sólo que el patrón de líneas variará de un instante a otro del tiempo, es decir, las líneas de campo al igual que las cargas serán móviles.
Campo electrodinámico (movimiento uniforme)
El campo eléctrico creado por una carga puntual presenta isotropía espacial, en cambio, el campo creado por una carga en movimiento tiene un campo más intenso en el plano perpendicular a la velocidad de acuerdo a las prediciones de la teoría de la relatividad. Esto sucede porque para un observador en reposo respecto a una carga que se mueve con velocidad uniforme la distancia en la dirección del movimiento de la carga serán menores que las medidas por un observador en reposo respecto a la carga, por efecto de la contracción de Lorentz, suponiendo que la carga se mueve a lo largo del eje X de observador tendríamos la siguiente relación de coornadas entre lo medido por el observador en movimiento respecto a la carga
 y el observador en reposo respecto a la carga
y el observador en reposo respecto a la carga  :
:
Sinedo V la velocidad de la carga respecto al observador, así la distancia efectiva a la carga medida por el observador en movimiento respecto a la carga cumplirá que:

Y por tanto el campo eléctrico medido por un observador en movimiento respecto a la carga será:
(19)

Donde
 es el ángulo formado por el vector de posición del punto donde se mide el campo (respecto a la carga) y la velocidad del movimiento. De esta última expresión se observa que si se considera una esfera de radio r alrededor de la carga el campo es más intenso en el "ecuador", tomando como polos norte y sur la interasección de la esfera con la trayectoria de la partícula, puede verse que el campo sobre la esfera varía entre un máximo
es el ángulo formado por el vector de posición del punto donde se mide el campo (respecto a la carga) y la velocidad del movimiento. De esta última expresión se observa que si se considera una esfera de radio r alrededor de la carga el campo es más intenso en el "ecuador", tomando como polos norte y sur la interasección de la esfera con la trayectoria de la partícula, puede verse que el campo sobre la esfera varía entre un máximo  y un mínimo
y un mínimo  dados por:
dados por:(20)

Esta pérdida de simetría esférica es poco notoria para velocidades pequeñas comparadas con la velocidad de la luz y se hace muy marcada a velocidades cercanas a la luz.
Campo electrodinámico (movimiento acelerado)
El campo de una carga en movimiento respecto a un observador se complica notablemente respecto al caso de movimiento uniforme si además de un movimiento relativo la carga presenta un movimiento acelerado respecto a un observador inercial. A partir de los potenciales de Lienard-Wiechert se obtiene que el campo creado por una carga en movimiento viene dado por:
(21)
![\bold{E} = \frac{1}{4\pi\epsilon} \left[
\frac{q(1-\frac{v^2}{c^2})}{(r-\frac{\bold{r}\cdot\bold{v}}{c})^3}(\bold{r}-\frac{\bold{v}}{c}r) +
\frac{q}{c^2(R-\frac{\bold{r}\cdot\bold{v}}{c})^3} \left[ \bold{r}
\times \left( (\bold{r}-\frac{\bold{v}}{c}r) \times \dot{\bold{v}} \right) \right]
\right]](b/8cb721fac4318c480449c45573f049cc.png)
El primer miembro sólo depende de la velocidad y coincide con el campo eléctrico provocado por una carga en movimiento uniforme, a grandes distancias varía según una ley de la inversa del cuadrado 1/R2 y, por tanto, no supone emisión de energía, el segundo miembro depende de la aceleración
 y tiene una variación 1/R que representa la intensidad decreciente de una onda esférica de radiación electromagnética, ya que las cargas en movimiento acelerado emiten radiación.
y tiene una variación 1/R que representa la intensidad decreciente de una onda esférica de radiación electromagnética, ya que las cargas en movimiento acelerado emiten radiación.Energía del campo eléctrico
Un campo en general almacena energía y en el caso de cargas aceleradas puede transmitir también energía (principio aprovechado en antenas de telecomunicaciones). La densidad volumétrica de energía de un campo eléctrico está dada por la expresión siguiente:[1]
(22)

Por lo que la energía total en un volumen V está dada por:
(23)

donde dV es el diferencial de volumen.
Véase también
- Ley de Coulomb
- Campo magnético
- Campo electromagnético
- Campo electrostático
- Densidad de carga
- Ecuaciones de Maxwell
- Ley de Gauss
- Potencial eléctrico
- Radiación electromagnética
- Campos dependientes del tiempo
- Electrodinámica cuántica
Referencias
Enlaces externos
Categorías:- Magnitudes electromagnéticas
- Electrostática
- Electrodinámica
Wikimedia foundation. 2010.