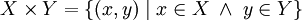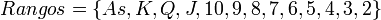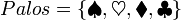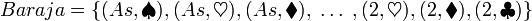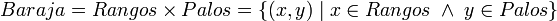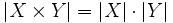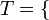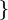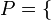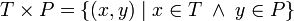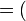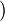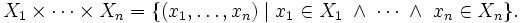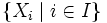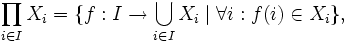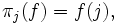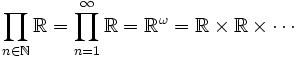- Producto cartesiano
-
Producto cartesiano
En teoría de conjuntos, el producto cartesiano es un producto directo de conjuntos. En particular, el producto cartesiano de dos conjuntos X y Y, denotado por X × Y, es el conjunto de todos los pares ordenados en los que el primer componente pertenece a X y el segundo a Y:
El producto cartesiano recibe su nombre de René Descartes, cuya formulación de la geometría analítica dio origen a este concepto.
Contenido
Ejemplo 1
El producto cartesiano del conjunto de trece rangos de la baraja inglesa
con el de los cuatro palos:
conjunto de las 52 cartas de la baraja:
la forma matemática de expresarlo es:
Si los conjuntos involucrados son finitos, la cardinalidad (o número de elementos) del producto cartesiano es el producto de las cardinalidades de los conjuntos involucrados:
En el ejemplo anterior, el número de elementos del producto era 52 = 13·4.
Ejemplo 2





























Partiendo de los conjuntos T de tubos de pintura y P de pinceles:
El producto cartesiano de estos dos conjuntos será:
En el cuadro hemos representado el conjunto T en la fila inferior y el P en la columna de la izquierda, en el cuadro donde se cortan la columna de cada tubo y la fila de cada pincel esta el par ordenado tubo pincel del color correspondiente.
Aunque en la figura no se representa téngase en cuenta que son pares ordenados y que el primer elemento corresponde al tubo y el segundo al pincel:
La representación en Coordenadas cartesianas de dos y tres dimensiones es una forma usual de representar el producto cartesiano de dos y tres conjuntos.
Generalización finita
El cuadrado cartesiano de un conjunto X se define como X2 = X × X. Un ejemplo de esto es el espacio euclídeo de dos dimensiones R2 = R × R, donde R es el conjunto de los números reales; R2 es entonces el conjunto de todos los puntos (x, y) donde x y y son ambos reales.
Esto se puede generalizar a un producto cartesiano n-ario sobre n conjuntos X1,..., Xn:
Este conjunto se puede identificar con (X1 ×... × Xn-1) × Xn; es un conjunto de n-tuplas.
Análogamente al cuadrado cartesiano, se pueden usar potencias mayores: R3 = R × R × R es el espacio euclídeo tridimensional.
Productos arbitrarios
La definición anterior usualmente basta para las aplicaciones matemáticas comunes. En algunos casos, sin embargo, puede ser necesario definir el producto cartesiano de una colección arbitraria (tal vez infinita) de conjuntos, y un intento de generalizar la definición de arriba a unas "tuplas inmensas" no tendría suficiente formalidad matemática.
Si I es cualquier conjunto, y si
es una colección de conjuntos, se define
esto es, la colección de todas las funciones definidas en el conjunto I cuyo valor en un índice cualquiera i es un elemento de Xi.
Para todo j ∈ I, la función
definida por
se denomina proyección sobre la coordenada j.
Una n-tupla puede también verse como una función definida en {1, 2,..., n}, cuyo valor en i es el i-ésimo elemento de la tupla. Con esto, si I = {1, 2,..., n}, la nueva definición coincide con la vieja.
Un caso particular del producto infinito ocurre cuando el conjunto índice es N, el conjunto de los naturales; en este caso, el producto es sencillamente el conjunto de secuencias infinitas cuyo i-ésimo término pertenece a Xi. De nuevo se puede ver un ejemplo con R:
es la colección de secuencias infinitas de números reales, y fácilmente se puede ver como un vector con infinitas componentes.
También es de notar el caso en el que todos los conjuntos "factores" Xi son iguales (ilustrado también por el ejemplo anterior). En este caso, la gran unión en la definición es sólo el único factor, y la segunda condición siempre se cumple; por lo tanto, el producto es solamente el conjunto de todas las funciones con dominio I y rango X, denotado XI por analogía con los "exponentes cartesianos".
En otros casos, el producto cartesiano infinito es menos intuitivo, aunque muy valioso por sus aplicaciones en la matemática.
La afirmación de que el producto cartesiano de una colección arbitraria de conjuntos no vacíos tampoco es vacío es equivalente al axioma de elección.
Teoría de la categoría
En la teoría de categorías, el producto cartesiano no es más que el producto en la categoría de conjuntos.
Véase también
Categoría: Teoría de conjuntos
Wikimedia foundation. 2010.