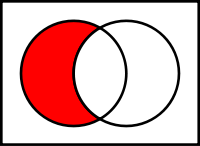
- Condicional material
-
El condicional material, también conocido como implicación material, condicional funcional de verdad o simplemente condicional, es una constante lógica que conecta dos proposiciones. El condicional material intenta ser la versión formal del condicional en el lenguaje natural, el cual se expresa por medio de palabras como las siguientes:
- Si llueve, entonces voy al cine.
- Voy al cine si llueve.
- Cuando llueve, voy al cine.
Simbólicamente, el condicional material se suele denotar de las siguientes maneras:

 , y en ocasiones:
, y en ocasiones:
Donde A y B son proposiciones cualesquiera. Las variables A y B se conocen respectivamente como el antecedente y el consecuente del condicional.
En lógica proposicional, el condicional material es una función de verdad binaria, que devuelve falso cuando A es verdadera y B es falsa, y devuelve verdadero en cualquier otro caso. En lógica de predicados, puede ser visto como una relación de subconjunto entre la extensión de predicados (posiblemente complejos).
Contenido
Definición
El condicional material es una función de verdad que toma dos valores de verdad (por lo general los valores de proposiciones) y devuelve falso cuando el primer valor es verdadero y el segundo falso, y verdadero en cualquier otro caso.
En otras palabras, la tabla de verdad del condicional material es la siguiente:
Como se ve, el condicional material devuelve 0 (falso) sólo cuando el antecedente es verdadero y el consecuente falso. En todos los demás casos, devuelve 1 (verdadero).
Propiedades formales
Algunas de las propiedades formales del condicional material son:
- Conmutatividad:

- Preservación de la verdad: La interpretación en virtud del cual todas las variables se les asigna un valor de verdad de «verdadero» produce un valor de verdad de «verdadero» como resultado de la implicación material.
Diferencia entre el condicional material y la implicación lógica
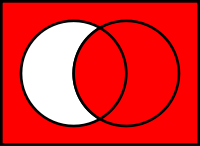 Diagrama de Venn del condicional material.
Diagrama de Venn del condicional material.
El condicional material no debe confundirse con la relación de implicación lógica. Sin embargo, existe una estrecha relación entre ambos en la mayoría de los sistemas lógicos, incluyendo la lógica clásica. Por ejemplo, los siguientes principios se sostienen:
- Si
 , entonces
, entonces  , donde A es una fórmula cualquiera y Γ es un conjunto de fórmulas cualquiera. Este es un caso particular del teorema de la deducción.
, donde A es una fórmula cualquiera y Γ es un conjunto de fórmulas cualquiera. Este es un caso particular del teorema de la deducción.
- Si
 , entonces
, entonces  . Esto es un caso particular del inverso del teorema de la deducción.
. Esto es un caso particular del inverso del teorema de la deducción.
- Tanto el condicional material como la consecuencia lógica son monótonas. Es decir, si
 , entonces
, entonces  y si
y si  , entonces
, entonces  .
.
Estos principios, sin embargo, no valen en todos los sistemas lógicos. Por ejemplo, no se sostienen en las lógicas no monotónicas.
La diferencia entre el condicional material y la implicación lógica es análoga la diferencia entre la operación
 y la operación
y la operación  en la teoría de conjuntos.
en la teoría de conjuntos.Ejemplo
En el camino de
 a
a  la diferencia entre la implicación lógica
la diferencia entre la implicación lógica  y material
y material  se puede ver en un cálculo fácil:
se puede ver en un cálculo fácil:El condicional material puede ser definido por medio de la disyunción y la negación. La relación
 por
por  y el cuantificador universal
y el cuantificador universal 
Problemas filosóficos en torno al condicional material
El significado de condicional material a veces puede ser usado en el idioma natural Inglés "si condición, entonces las consecuencias" de la construcción (una especie de condena condicional), donde la condición y la consecuencia es que se llena de frases Inglés. Sin embargo, esto también implica la construcción de una "razonable" la conexión entre la condición (prótasis) y la consecuencia (apódosis) (ver la lógica Connexive).
Así, a pesar de un condicional material de una contradicción es siempre así, en lenguaje natural, "Si hay tres átomos de hidrógeno en H2O entonces el gobierno perderá las próximas elecciones" se interpreta como falso por la mayoría de los oradores, ya que las afirmaciones de la química se consideran irrelevantes condiciones de proponer consecuencias políticas. "Si P entonces Q", en lenguaje natural, parece significar "P y Q están conectados y P → Q". ¿Qué clase de relación que se entiende por lenguaje natural no está claramente definido.
La declaración "if (B) todos los solteros no están casados, entonces (C) la velocidad de la luz en el vacío es constante", se puede considerar falsa, porque no hay ninguna conexión perceptible entre la (B) y (C), a pesar de que (B) → (C) es verdadera. La declaración "if (S) Sócrates era una mujer, entonces (T) 1 +1 = 3" se puede considerar falsa, por la misma razón, a pesar de (S) → (T) es verdadera. Cuando prótasis y apódosis están conectados, la funcionalidad de la verdad de los condicionales lingüística y lógica coinciden: la distinción es sólo aparente cuando el material condicional es verdadero, pero su antecedente y el consecuente son percibidos como ajenos.
El material modificador de material condicional hace la distinción de los condicionales lingüísticos explícitos. Se aísla la relación subyacente, la verdad funcional inequívoca. Por lo tanto, la encapsulación exacta del lenguaje natural de los materiales condicional X → Y, de forma aislada, se ve que "es falso que X es verdad, mientras que Y falsa" o "no puede ser que X y no Y-" - es decir, en símbolos,.
La función corresponde a la verdad no ... o ... » y no se corresponde con el Inglés "si ... entonces ..." de la construcción. Por ejemplo, cualquier declaración condicional con un antecedente falso es verdadero.
Así que la afirmación "si 2 es impar, entonces 2 es aún" es cierto. Del mismo modo, cualquier material condicional con un verdadero consecuente es verdadero. Así que la declaración, "si los cerdos vuelan y luego a París está en Francia" es cierto. Estos problemas se conocen como las paradojas de la implicación material, aunque en realidad no son paradojas en el sentido estricto, es decir, que no provoca contradicciones lógicas.
Hay varios tipos de condicionales en Inglés, por ejemplo, no es el condicional indicativo y el subjuntivo condicional o hipotética. Estos últimos no tienen la mismas condiciones de verdad como el material condicional. Para una visión general de algunos análisis de los diversos, formales e informales, de los condicionales, consulte la sección "Referencias" más adelante.
Véase también
Referencias
- Este artículo fue creado a partir de la traducción del artículo Material conditional de la Wikipedia en inglés, concretamente de esta versión, bajo licencia Creative Commons Atribución Compartir Igual 3.0 y GFDL.
Bibliografía
- Brown, Frank Markham (2003). Razonamiento booleanos: La lógica de las ecuaciones booleanas (2ª edición). Nueva York: Dover Publications.
- Edgington, Dorothy (2001), «Condicionales», en Lou Goble, The Blackwell Guide to Philosophical Logic, Blackwell
- Edgington, Dorothy, «Conditionals», en Edward N. Zalta (en inglés), The Stanford Encyclopedia of Philosophy (Winter 2008 Edition), http://plato.stanford.edu/archives/win2008/entries/conditionals/
- Quine, Willard van Orman (1982). Métodos de la lógica (4ª edición). Cambridge: Harvard University Press.
- Stalnaker, Robert (1975). «Condicionales indicativos». Philosophia 5: pp. 269-286.
Wikimedia foundation. 2010.