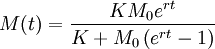- Curva logística
-
Curva logística
La curva logística o curva en forma de S es una función matemática que aparece en diversos modelos de crecimiento de poblaciones, propagación de enfermedades epidémicas y difusión en redes sociales. Dicha función constituye un refinamiento del modelo exponencial para el crecimiento de una magnitud.
La curva logística propone que bajo ciertas circunstancias razonables muchas magnitudes en sistemas ecológicos y sociales evolucionan con el tiempo de acuerdo con la expresión:
Donde K es se llama capacidad del sistema, y r se llama tasa natural de incremento. Una magnitud que crece de acuerdo con esa expresión se dice que presenta crecimiento logístico.Propiedades
La función logística que modeliza el crecimiento logístico de una magnitud M(t) tiene las siguientes propiedades:
- Crecimiento acotado, para todo t se cumple que:
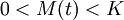
- Aproximación exponencial, para valores pequeños de M/K (o también para valores de
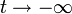 la función logística puede aproximarse por un modelo de crecimiento exponencial del tipo
la función logística puede aproximarse por un modelo de crecimiento exponencial del tipo 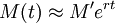 .
.
Origen del crecimiento logístico
El crecimiento logístico está relacionado con el crecimiento exponencial, de hecho para pequeños valores de la magnitud que presenta crecimiento logístico, el crecimiento logístico se asemeja mucho al crecimiento exponencial. Sin embargo, a partir de un cierto punto el crecimiento se ralentiza, eso hace que la curva pueda representar adecuadamente la propagación de rumores, la extensión de una innovación tecnológica o una epidemia: al principio estas se propagan rápidamente, cada "infectado" o "afectado" por la innovación es susceptible de traspasar el "contagio" a otro individuo que tenga contacto con él, pero a cuando el número de "infectados" crece es más difícil encontrar una persona que previamente no haya estado en contacto con la enfermedad o innovación.
Una mangitud P; que sigue un crecimiento logístico tiene un crecimiento dado por la ecuación diferencial no lineal:
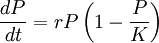
Donde:
 , es la tasa de crecimiento, cuando P; es pequeña en relación a
, es la tasa de crecimiento, cuando P; es pequeña en relación a 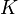 la tasa de crecimiento de la variable es prácticamente proporcional a r, tal como sucede en un modelo de crecimiento exponencial.
la tasa de crecimiento de la variable es prácticamente proporcional a r, tal como sucede en un modelo de crecimiento exponencial.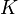 es la capacidad o nivel de saturación de la variable, normalmente representa alguna restricción que el ecosistema o el medio en el que crece la variable impone un límite máximo por encima del cual la variable no puede seguir creciendo.
es la capacidad o nivel de saturación de la variable, normalmente representa alguna restricción que el ecosistema o el medio en el que crece la variable impone un límite máximo por encima del cual la variable no puede seguir creciendo.
Categorías: Wikipedia:Fusionar | Ecosistema | Investigación social | Ecuaciones diferenciales ordinarias
Wikimedia foundation. 2010.