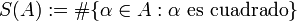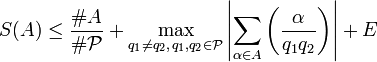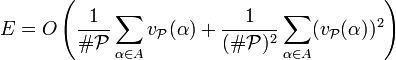Criba de cuadrados

Criba de cuadrados

Saltar a navegación, búsqueda

La criba de cuadrados es una técnica en teoría de cribas usada para estimar la cantidad de cuadrados en un conjunto de enteros, este recae sobre el uso de símbolos de residuos cuadráticos para cribar dichos cuadrados. Como consecuencia, esta obtiene buenos estimativos para aquellas secuencias que son uniformente distribuidas.

La criba de cuadrados asegura:

Sea A un conjunto de enteros diferentes de cero, sea 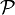$\mathcal{P}$ el conjunto de primos impares en A. Sea

$S(A):=\#\{\alpha\in A:\alpha\mbox{ es cuadrado}\}$

Entonces, la criba afirma que

$S(A)\leq\frac{\# A}{\# \mathcal{P}}+\max_{q_{1}\neq q_{2},\,q_{1},q_{2}\in\mathcal{P}}\left|\sum_{\alpha\in A}\left(\frac{\alpha}{q_{1}q_{2}}\right)\right|+E$

Donde (·/q₁q₂) es el símbolo de Jacobi y

$E=O\left(\frac{1}{\# \mathcal{P}}\sum_{\alpha\in A}v_{\mathcal{P}}(\alpha)+\frac{1}{(\# \mathcal{P})^2}\sum_{\alpha\in A}(v_{\mathcal{P}}(\alpha))^2\right)$

Y la función v_P(n) cuanta la cantidad de factores primos de n en $\mathcal{P}$.

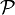La contribución del término E es insignificante en la práctica.

Véase

• Teoría de cribas
• Criba de Atkin

Referencias

• Alina Carmen Cojocaru; M. Ram Murty. An introduction to sieve methods and their applications (vol. 66). Cambridge University Press, pp. 135–155. ISBN 0-521-61275-6.

Obtenido de "Criba de cuadrados"