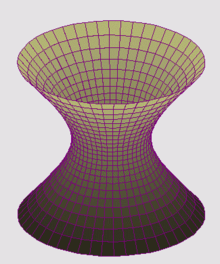
Cuádrica

Una cuádrica es una superficie determinada por una ecuación de la forma: $P(x_1,x_2 ... x_n) = 0 \$

donde P es un polinomio de segundo grado en las coordenadas $x_1, x_2 ... x_n \$.

Cuando no se precisa, es una superficie del espacio tridimensional real usual, en un sistema de coordenadas ortogonal y unitario, y las coordenadas se llaman x, y, z.

Hiperboloide de una hoja.

Historia

Fueron los matemáticos griegos de la antigüedad quienes iniciaron el estudio de las cuádricas, con el cono (una cuádrica) y sus secciones, que son las cuádricas en el plano bidimensional, aunque no emplearon ecuaciones.

Definición algebraica

Una cuádrica o superficie cuádrica, es una hipersuperficie D-dimensional representada por una ecuación de segundo grado con variables (coordenadas) espaciales. Si estas coordenadas son $\{x_1, x_2, ... x_D\}\,$, entonces la cuádrica típica en ese espacio se define mediante la ecuación algebraica:

$\sum_{i,j=1}^D Q_{i,j} x_i x_j + \sum_{i=1}^D P_i x_i + R = 0$

donde Q es una matriz cuadrada de dimensión (D), P es un vector de dimensión (D) y R es una constante. Si bien Q, P y R son por lo general reales o complejos, una cuádrica puede definirse en general sobre cualquier anillo.

Ecuación cartesiana

La ecuación cartesiana de una superficie cuádrica es de la forma:

$Ax^2 + By^2 + Cz^2 + Dxy + Eyz + Fxz + Gx + Hy + Iz + J = 0 \,$

• La definición algebraica de las cuádricas tiene el defecto de incluir casos sin interés geométrico y sin vínculo con el tema.

Por ejemplo, la ecuación:

$x^2 + y^2 + z^2 +2xy + 2yz + 2xz = 0 \$

es de segundo grado pero, también se puede escribir como:

$(x+y+z)^2 = 0 \$

que equivale a:

$x + y + z = 0 \$,

una ecuación de primer grado que corresponde a un plano, superficie que no tiene las propiedades relacionadas con el segundo grado. Generalmente, se descartan todos los polinomios de segundo grado que son cuadrados.

Ecuación normalizada

La ecuación normalizada de una cuádrica tridimensional (D = 3), centrada en el origen (0, 0, 0) de un espacio tridimensional, es:

$\pm {x^2 \over a^2} \pm {y^2 \over b^2} \pm {z^2 \over c^2} \pm 1 = 0$

Tipos de cuádricas

Por medio de traslaciones y rotaciones cualquier cuádrica se puede transformar en una de las formas "normalizadas". En el espacio tridimensional euclídeo, existen 16 formas normalizadas; las más interesantes son las siguientes:

elipsoide	${x^2 \over a^2} + {y^2 \over b^2} + {z^2 \over c^2} - 1 = 0 \,$
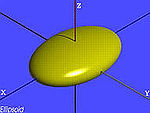
→ esferoide (caso particular de elipsoide)	${x^2 \over a^2} + {y^2 \over a^2} + {z^2 \over b^2} - 1 = 0 \,$
→ esfera (caso particular de esferoide)	${x^2 \over a^2} + {y^2 \over a^2} + {z^2 \over a^2} - 1 = 0 \,$
paraboloide
→ paraboloide hiperbólico (caso particular de paraboloide)	${x^2 \over a^2} - {y^2 \over b^2} - z = 0 \,$
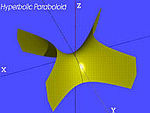
→ paraboloide elíptico (caso particular de paraboloide)	${x^2 \over a^2} + {y^2 \over b^2} - z = 0 \,$
→ paraboloide circular (caso particular de paraboloide elíptico)	${x^2 \over a^2} + {y^2 \over a^2} - z = 0 \,$
hiperboloide
→ hiperboloide de una hoja (caso particular de hiperboloide)	${x^2 \over a^2} + {y^2 \over b^2} - {z^2 \over c^2} - 1 = 0 \,$
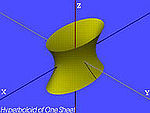
→ hiperboloide de dos hojas (caso particular de hiperboloide)	${x^2 \over a^2} + {y^2 \over b^2} - {z^2 \over c^2} + 1 = 0 \,$
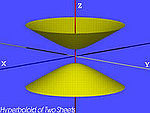
cilindro
→ cilindro elíptico (caso particular de cilindro)	${x^2 \over a^2} + {y^2 \over b^2} - 1 = 0 \,$
→ cilindro circular (caso particular de cilindro elíptico)	${x^2 \over a^2} + {y^2 \over a^2} - 1 = 0 \,$
→ cilindro hiperbólico (caso particular de cilindro)	${x^2 \over a^2} - {y^2 \over b^2} - 1 = 0 \,$
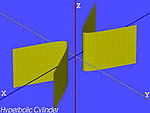
→ cilindro parabólico (caso particular de cilindro)	$x^2 + 2ay = 0 \,$
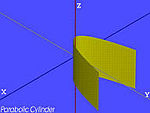
cono elíptico	${x^2 \over a^2} + {y^2 \over b^2} - {z^2 \over c^2} = 0 \,$
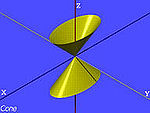
→ cono circular (caso particular de cono elíptico)

En el espacio proyectivo real, el elipsoide, el hiperboloide elíptico y el paraboloide elíptico son similares; los dos paraboloides hiperbólicos tampoco se diferencian entre ellos (por ser superficies regladas; el cono y el cilindro tampoco son distintos entre sí (por ser cuádricas "degeneradas"). En el espacio proyectivo complejo todas las cuádricas no degeneradas resultan indistinguibles entre ellas.

Véase también

• Cónica

Enlaces externos

• Cuádricas, en wmatem.eis.uva.es
• El contenido de este artículo incorpora material de una entrada de la Enciclopedia Libre Universal, publicada en español bajo la licencia Creative Commons Compartir-Igual 3.0.