- Cuerpo de descomposición
-
Cuerpo de descomposición
En álgebra abstracta, se puede considerar el cuerpo de descomposición de un polinomio (o familia de polinomios) o de un cuerpo.
Cuerpo de descomposición de un polinomio
Dado un cuerpo K, y un polinomio no constante
![p(x)\in K[x]](/pictures/eswiki/98/b9db1f17d508db907f0a85c531f5be53.png) (i.e., con coeficientes en K) de grado n, se define el cuerpo de descomposición de p como un cuerpo Ep que cumple:
(i.e., con coeficientes en K) de grado n, se define el cuerpo de descomposición de p como un cuerpo Ep que cumple:- Que el polinomio p(x) descompone completamente en Ep, es decir, que se puede expresar p(x) como
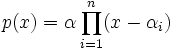 , con
, con 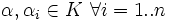
- Que el cuerpo sea minimal con la propiedad anterior.
Es decir, el cuerpo de descomposición es el que resulta de adjuntar a K todas las raíces del polinomio p(x): Ep = K(α1,α2,...,αn).
Cuerpo de descomposición de una familia de polinomios
El cuerpo de descomposición de una familia de polinomios
![T\subseteq K[x]](/pictures/eswiki/52/4b34917577f6dffd1367576b758c8f8b.png) es, análogamente a lo anteriormente expuesto, el cuerpo minimal en el que descomponen completamente todos los polinomios
es, análogamente a lo anteriormente expuesto, el cuerpo minimal en el que descomponen completamente todos los polinomios ![p(x)\in T \subseteq K[x]](/pictures/eswiki/102/f66ea179b36d03cf268da6c0c259ade4.png) .
.Cuerpo de descomposición de un cuerpo
Dado un cuerpo K, el cuerpo de descomposición de K es el cuerpo de descomposición de la familia de polinomios K[x]; es decir, el cuerpo que contiene todas las raíces de todos los polinomios con coeficientes en K.
En este caso se le llama clausura algebraica de K y se le denota por
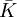 .
.Se cumple que cualquier cuerpo Ω algebraicamente cerrado que contenga a K, también contiene a
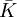 :
: 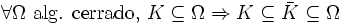 Categoría: Teoría de cuerpos
Categoría: Teoría de cuerpos
Wikimedia foundation. 2010.
