- Curva
-
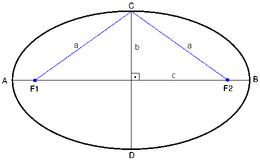
En matemáticas, el concepto de curva (o línea curva) es una línea continua de una dimensión, que varía de dirección paulatinamente. Ejemplos sencillos de curvas cerradas son la elipse o la circunferencia, y de curvas abiertas la parábola, la hipérbola o la catenaria. La recta sería el caso límite de una círculo de radio de curvatura infinito. Todas las curvas tienen dimensión topológica igual a 1.
Contenido
Historia y definiciones
Cronología[1] Año Acontecimiento 300 a. C. Euclides define las secciones cónicas 250 a. C. Arquímedes investiga las curvas espirales. 225 a. C.. Apolonio de Perge publica Cónicas. 1704 Isaac Newton clasifica las curvas cónicas. 1890 Giuseppe Peano aplicando la definición de Jordán,
demuestra que un cuadrado relleno también es una curva.Década de 1920 Pável Urysón y Karl Menger definen el concepto de curva a partir de la topología. Camille Jordan (1838-1922) propuso una teoría sobre las curvas basada en la definición de una curva en términos de puntos variables (ver teorema de la curva de Jordan. En geometría, una curva en el n-espacio euclideano es un conjunto
 que es la imagen de un intervalo Ι abierto bajo una aplicación diferenciable
que es la imagen de un intervalo Ι abierto bajo una aplicación diferenciable  , i.e:
, i.e:
donde suele decirse que (
 ) es una representación paramétrica o parametrización de
) es una representación paramétrica o parametrización de  .
.Las curvas, según esta definición, pueden ser muy intrincadas, de muy diverso tipo. Con el objetivo de evitar auto intersecciones, puntos singulares y a los extremos, se define el concepto de curva simple como aquella curva tal que para todo punto p existe un Ω entorno abierto de p para el cual
 admite una representación de clase Ck con
admite una representación de clase Ck con  .
.La definición de Jordan ha sido cuestionada a partir del descubrimiento del italiano Giuseppe Peano. Este matemático demostró en 1890 que un cuadado relleno entra dentro de la definición de Jordan, pues logró representar todos los puntos del mismo utilizando dicha definición: trazó todos los puntos del cuadrado con una única curva. Pero es claro que un cuadrado no es, en el sentido convencional del término, una curva. Debido a ello, y al descubrimiento posterir de otros casos similares a los de Peano, se ha planteado la necesidad de mejorar la definición de la definición de lo que es, matemáticamente, una curva.[1]
Curva diferenciable
Una curva se llama diferenciable cuando la función
![\mathbf{x}\colon [a,b] \subset \Iota \to\mathbb{R}^n](a/1fa70f964eba9b935214b85b26bd4725.png) es diferenciable. Si además la función anterior es inyectiva en el intervalo
es diferenciable. Si además la función anterior es inyectiva en el intervalo  entonces la curva admite un vector tangente único en cada punto y es rectificable (lo cual significa que su longitud de arco está bien definida y es posible calcular su longitud. La curva
entonces la curva admite un vector tangente único en cada punto y es rectificable (lo cual significa que su longitud de arco está bien definida y es posible calcular su longitud. La curva  :
:
es continua pero no diferenciable, por lo qu esu longitud entre el punto (0,0) y cualquier otro punto de la misma no puede calcularse.
Curva cerrada
Una curva diferenciable es cerrada cuando
![\mathbf{x}\colon [a,b] \to\mathbb{R}^n](d/bddfb71f27f4ae44ee9eb8eb5c7e82d7.png) cuando
cuando  . Si además, la función
. Si además, la función  es inyectiva en el intervalo
es inyectiva en el intervalo  entonces se dice que la curva es una curva cerrada simple. Una curva cerrada simple es homeomorfa al círculo S1, es decir, tiene la misma topología de un anillo. La curva
entonces se dice que la curva es una curva cerrada simple. Una curva cerrada simple es homeomorfa al círculo S1, es decir, tiene la misma topología de un anillo. La curva ![\mathbf{x}\colon [0,1] \to\mathbb{R}^n](9/c392db75933b2b1aa3bba6f4849dc8f5.png) dada por:
dada por:
es una curva diferenciable cerrada, de hecho dicha curva resulta ser una elipse de semiejes a y b.
Geometría diferencial de curvas en R3
La geometría diferencial de curvas propone definiciones y métodos para analizar curvas simples en el espacio euclídeo tridimensional o, más generalmente, curvas contenidas en variedades de Riemann. En particular, en el espacio euclídeo tridimensional
 , una curva de la que se conoce un punto de paso y el vector tangente en dicho punto, queda totalmente descrita por su curvatura y torsión. Esta curvatura y torsión pueden estudiarse mediante el llamado triedro de Frênet-Serret, que se explica a continuación.
, una curva de la que se conoce un punto de paso y el vector tangente en dicho punto, queda totalmente descrita por su curvatura y torsión. Esta curvatura y torsión pueden estudiarse mediante el llamado triedro de Frênet-Serret, que se explica a continuación.Vectores tangente, normal y binormal
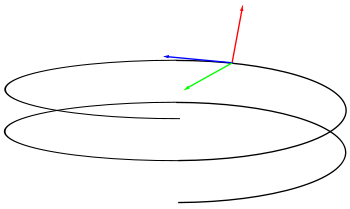 Vista esquemática del vector tangente (azul), vector normal (verde) y vector binormal (rojo) de una curva hélice.
Vista esquemática del vector tangente (azul), vector normal (verde) y vector binormal (rojo) de una curva hélice.
Dada una curva parametrizada r(t) según un parámetro cualquiera t se define el llamado vector tangente, binormal y normal como:
Estos tres vectores son unitarios y perpendiculares entre sí, juntos configuran un sistema de referencia móvil conocido como triedro de Frênet-Serret. Es interesante que para una partícula física desplazándose en el espacio, el vector tangente es paralelo a la velocidad, mientras que el vector normal da el cambio dirección por unidad de tiempo de la velocidad o aceleración normal.Curvas no diferenciables
 Porción de una curva de Koch, la extrema rugosidad que presenta hace que su dimensión fractal sea 1,261... > 1. Aunque como curva su dimensión topológica sigue siendo 1.
Porción de una curva de Koch, la extrema rugosidad que presenta hace que su dimensión fractal sea 1,261... > 1. Aunque como curva su dimensión topológica sigue siendo 1.
Cuando la función que define la curva es diferenciable se dice que la curva es diferenciable. Una curva diferenciable tiene la propiedad de admitir una recta tangente en cada uno de sus puntos. Una curva con un número finito de puntos donde no es diferenciable es una curva diferenciable a tramos. Cuando el número de puntos no es finito puede darse el caso de una curva continua no sea rectificable en ningún punto, eso significa que la tangente no puede definirse en ningún punto. En esos casos la longitud de la curva no es un número finito y puede darse el caso que la curva tenga una longitud infinita aun cuando ocupe una región finita del espacio. La curva de Koch es un ejemplo de curva no recticable de longitud infinita, que encierra un área finita. De hecho esta curva es un objeto fractal de dimensión fractal:

Referencias
- ↑ a b Tony Crilly (2011). 50 cosas que hay que saber sobre matemáticas. Ed. Ariel. ISBN 978-987-1496-09-9.
Enlaces externos
 Wikimedia Commons alberga contenido multimedia sobre curvas. Commons
Wikimedia Commons alberga contenido multimedia sobre curvas. Commons Wikcionario tiene definiciones para curva.Wikcionario
Wikcionario tiene definiciones para curva.Wikcionario
Categorías:- Curvas
- Topología
- Geometría métrica
Wikimedia foundation. 2010.