- Curva integral de un campo vectorial
-
Curva integral de un campo vectorial
En matemáticas, una curva integral de un campo vectorial es el análogo abstracto de la línea de corriente en el flujo de un fluido. En física cuando el campo en cuestión representa un campo de fuerzas las curvas integrales corresponden a las líneas de fuerza.
Definición
Dado un campo vectorial
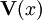 definido en algún conjunto abierto A en el espacio euclídeo, o más generalmente en una variedad diferenciable
definido en algún conjunto abierto A en el espacio euclídeo, o más generalmente en una variedad diferenciable 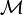 , una curva integral
, una curva integral 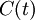 de
de 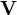 en un punto dado P de
en un punto dado P de 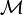 es la curva en
es la curva en 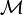 definida en un cierto intervalo [-a, a] con 0 < a, tal que
definida en un cierto intervalo [-a, a] con 0 < a, tal que![C:[-a,a]\to A \subset \mathcal{M}, \qquad \mbox{con}\quad C(0) = P](/pictures/eswiki/48/03b6e3d9f936a4e448e50cf949581524.png)
y tal que la derivada:
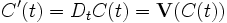
Esta última condición en la derivada equivale a que el vector tangente a la curva C sea precisamente el vector dado por V.
Propiedades
Además el conjunto de curvas integrales de una región constituye una foliación unidimensional de dicha región. Eso implica que dado un punto de esa región donde el campo no sea nulo, por ese punto pasa una y sólo una curva integral.
Esas propiedades de las curvas integrales, hacen posible visualizar un campo vectorial como dando lugar a un flujo en M, con cada punto moviéndose en la dirección vectorial dada por V, y en una tasa proporcional a su longitud. Si V tiene un cero en un punto Q, entonces Q será inmóvil (es decir la curva constante a Q será la curva integral). Esto es un flujo 'estacionario' (independiente del tiempo); como un modelo de una ecuación diferencial ordinaria, éste es el más simple posible, y las representaciones del espacio de fase se utilizan a menudo para construir tal campo vectorial auxiliar.
Desde un punto de vista matemático, puede haber problemas en extender una curva integral para tener como dominio el conjunto de la recta de los números reales. El flujo puede por ejemplo alcanzar el borde de M en un tiempo finito. Los usos típicos son el flujo geodésico, y subgrupos uniparamétricos y función exponencial en grupos de Lie.
Categoría: Cálculo integral
Wikimedia foundation. 2010.
