Deducción del módulo de la suma
- Deducción del módulo de la suma
-
Deducción del módulo de la suma
Este artículo presenta una deducción para la expresión del módulo resultante de dos vectores (véase Vector (física) y Módulo (vector))
Deducción
Sean dos vectores 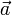 y
y 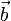 que forman un ángulo θ entre sí:
que forman un ángulo θ entre sí:
La fórmula para calcular 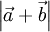 se deduce observando los triángulos rectángulos que se forman, OCB y ACB, y aplicando el Teorema de Pitágoras. En el triángulo OCB:
se deduce observando los triángulos rectángulos que se forman, OCB y ACB, y aplicando el Teorema de Pitágoras. En el triángulo OCB:
OB2 = OC2 + CB2
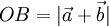
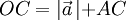
Resultando:
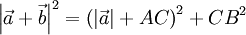
En el triángulo ACB :
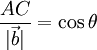
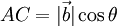
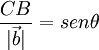
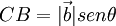
Sustituyendo esto en la igualdad de antes resulta:
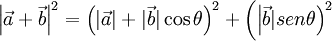
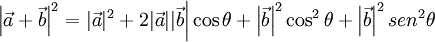
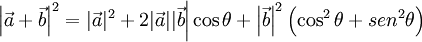
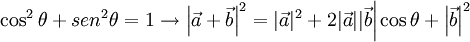
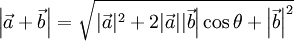
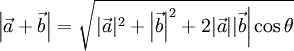
Categoría: Álgebra lineal
Wikimedia foundation.
2010.
Mira otros diccionarios:
Vector — Para otros usos de este término, véase Vector (desambiguación). Este artículo trata sobre el concepto físico de vector. Para el tratamiento matemático formal, véase Espacio Vectorial. Un vector desde A hasta B. En física, mate … Wikipedia Español
Vector (física) — Saltar a navegación, búsqueda Para otros usos de este término, véase Vector. Un vector es una magnitud física caracterizable mediante un módulo y una dirección u orientación, la cual puede ser representada en coordenadas polares o mediante la… … Wikipedia Español
Circuito eléctrico — Saltar a navegación, búsqueda Se denomina circuito eléctrico a una serie de elementos o componentes eléctricos o electrónicos, tales como resistencias, inductancias, condensadores, fuentes, y/o dispositivos electrónicos semiconductores,… … Wikipedia Español
Impuesto sobre la Renta de las Personas Físicas (España) — El Impuesto sobre la Renta de las Personas Físicas o IRPF, es un impuesto personal, progresivo y directo que grava la renta obtenida en un año natural por las personas físicas residentes en España. Así pues, es una figura impositiva perteneciente … Wikipedia Español
Criptoanálisis — Saltar a navegación, búsqueda Criptoanálisis (del griego kryptós, escondido y analýein, desatar ) es el estudio de los métodos para obtener el sentido de una información cifrada, sin acceso a la información secreta requerida para obtener este… … Wikipedia Español
Aproximación para campos gravitatorios débiles — Saltar a navegación, búsqueda La aproximación para campos gravitatorios débiles comprende la búsqueda de soluciones aproximadas de las ecuaciones del campo de Einstein de la teoría general de la relatividad. Contenido 1 Métrica aproximada para… … Wikipedia Español
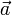 y
y 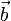 que forman un ángulo θ entre sí:
que forman un ángulo θ entre sí: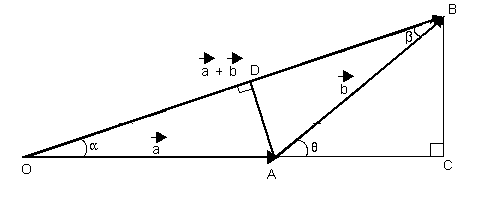
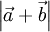 se deduce observando los triángulos rectángulos que se forman, OCB y ACB, y aplicando el Teorema de Pitágoras. En el triángulo OCB:
se deduce observando los triángulos rectángulos que se forman, OCB y ACB, y aplicando el Teorema de Pitágoras. En el triángulo OCB: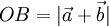
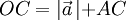
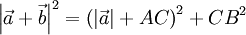
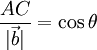
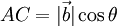
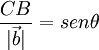
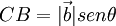
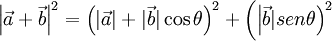
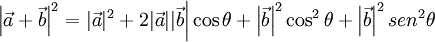
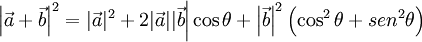
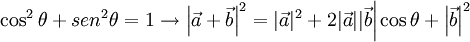
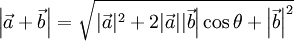
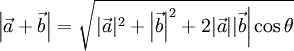 Categoría: Álgebra lineal
Categoría: Álgebra lineal