- Prueba de consistencia
-
Prueba de consistencia
En lógica matemática, un sistema formal es consistente si no contiene una contradicción, o, en forma más precisa, no existe una proposición φ tal que se puede demostrar o deducir simultáneamente la proposición φ y su contraria ¬φ o no-φ.
Referido a un argumento, la consistencia es la necesidad de que todas las premisas tengan que ser necesariamente y a la vez, como producto, todas verdaderas, para que el argumento, si es consistente, pueda ser válido o no válido. Referido al discurso la consistencia tiene que ver con que las implicaciones lógicas del mismo no sean autocontradictorias.
Una demostración de consistencia (o prueba de consistencia) es una demostración formal de que un sistema formal es consistente. El desarrollo inicial de la teoría de la demostración matemática fue motivado por el deseo de proveer demostraciones de consistencia finita para toda la matemáticas como parte del programa de Hilbert. El programa de Hilbert cumple con las observaciones de Gödel, tal como se expresa en sus dos teoremas de incompletitud de Gödel, de que las teorías de demostración robustas no son capaces de probar su propia consistencia.
A pesar de que es posible demostrar la consistencia mediante teoría de modelos, por lo general se realiza de una manera puramente sintáctica, sin la necesidad de proveer una referencia a algún modelo de la lógica. La eliminación de corte (o en forma equivalente la normalización del cálculo subyacente si es que existe uno) implica la consistencia del cálculo: dado que obviamente no existe prueba de falsedad que sea libre de corte, no existe por lo tanto contradicción en general.
Contenido
Consistencia y completitud
Los principales resultados relacionados con la consistencia y completitud fueron demostrados por Kurt Gödel:
- El teorema de completitud de Gödel indica que toda teoría de primer orden consistente es completa con respecto al conjunto consistente máximo de las fórmulas que se generan por medio del algoritmo de búsqueda de demostración.
- Los teoremas de la incompletitud de Gödel indican que las teorías capaces de expresar su propia relación de demostrabilidad y de desarrollar un argumento diagonal son capaces de demostrar su propia consistencia solo si son inconsistentes. Estas teorías, si son consistentes, son denominadas teorías esencialmente incompletas.
Mediante la aplicación de estas ideas, se pueden encontrar cuatro tipos distintos de teorías de primer orden:
- Teorías inconsistentes, que no poseen modelos;
- Teorías que no pueden analizar su propia relación de demostración, tales como la axiomatización de Tarski de la geometría del punto y la linea, y la aritmética de Presburg. Dado que estas teorías son descriptas en forma satisfactoria por el modelo que se obtiene mediante el teorema de completitud, entonces estos sistemas son completos;
- Teorías capaces de analizar su propia consistencia, y que incluyen la negación de la proposición que asevera su propia consistencia. Este tipo de teorías son completas con respecto al modelo que se obtiene a partir del teorema de completitud, pero contienen como teorema la implicancia de una contradicción, en contradicción al hecho de que son consistentes;
- Teorías esencialmente incompletas.
En forma adicional, se ha descubierto recientemente que existe un quinto tipo de teoría, las teorías auto verificables, que son lo suficientemente robustas como para analizar su propia relación de demostración, pero son demasiado débiles como para realizar una diagonalización de Gödel, y que por lo tanto pueden demostrar en forma consistente su propia consistencia. Sin embargo, una teoría que demuestra su propia consistencia no permite obtener ninguna información interesante, dado que las teorías inconsistentes también demuestran su propia consistencia.
Fórmulas
Un conjunto de fórmulas Φ en lógica de primer orden es consistente (expresado como ConΦ) si y solo si no existe una fórmula φ tal que
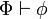 y
y 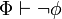 . De lo contrario Φ es inconsistente y se expresa IncΦ.
. De lo contrario Φ es inconsistente y se expresa IncΦ.Φ es simplemente consistente si y solo si para ninguna fórmula φ de Φ son tanto φ como la negación de φ teoremas de Φ.
Φ es absolutamente consistente o Post consistente si por lo menos una fórmula de Φ no es un teorema de Φ.
Φ es máximamente consistente si y solo si para toda fórmula φ, si Con
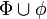 entonces
entonces 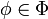 .
.Φ se dice contiene testigos si y solo si para cada fórmula de la forma
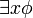 existe un término t tal que
existe un término t tal que 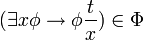 . Véase Lógica de primer orden.
. Véase Lógica de primer orden.Resultados básicos
1. Los siguientes son equivalentes:
(a) IncΦ
(b) Para todo
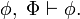
2. Todo conjunto de fórmulas satisfiable es consistente, un conjunto de fórmulas Φ es satisfiable si y solo si existe un modelo
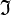 tal que
tal que 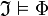 .
.3. Para todo Φ y φ:
(a) si no
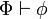 , entonces Con
, entonces Con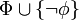 ;
;(b) si Con Φ y
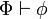 , entonces Con
, entonces Con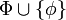 ;
;(c) si Con Φ, entonces Con
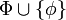 o Con
o Con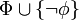 .
.4. Sea Φ un conjunto de fórmulas consistentes y que poseen testigos. Para todo φ y ψ:
(a) si
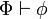 , entonces
, entonces 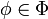 ,
,(b) o bien
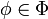 o bien
o bien 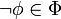 ,
,(c)
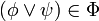 si y solo si
si y solo si 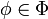 o
o 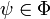 ,
,(d) si
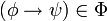 y
y 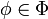 , entonces
, entonces 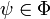 ,
,(e)
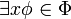 si y solo si existe un término t tal que
si y solo si existe un término t tal que 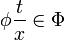 .
.Teorema de Henkin
Sea Φ un conjunto de fórmulas máximamente consistentes con testigos.
Define una relación binaria en el conjunto de términos S
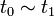 si y solo si
si y solo si 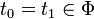 ; y sea
; y sea 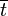 la clase de términos de equivalencia conteniendo
la clase de términos de equivalencia conteniendo 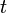 ; y sea
; y sea 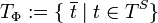 donde
donde 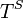 es el conjunto de términos basados en el conjunto de símbolo
es el conjunto de términos basados en el conjunto de símbolo 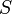 .
.Define la estructura S
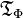 sobre
sobre 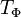 el término-estructura correspondiente a Φ mediante:
el término-estructura correspondiente a Φ mediante:(1) Para el n-ésimo
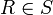 ,
, 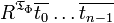 si y solo si
si y solo si 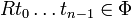 ,
,(2) Para el n-ésimo
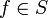 ,
, 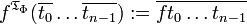 ,
,(3) Para
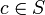 ,
, 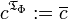 .
.Sea
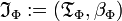 el término interpretación asociado con Φ, donde
el término interpretación asociado con Φ, donde 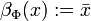 .
.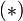 Para todo φ,
Para todo φ,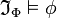 si y solo si
si y solo si 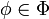 .
.Véase también
- Lógica paraconsistente
- Equiconsistency
- Hilbert's second problem
- Hilbert's program
- Hilbert's problems
- Matiyasevich's theorem
- Emil Post (1920)
- Łukasiewicz
Referencias
H.D. Ebbinghaus, J. Flum, W. Thomas, Mathematical Logic
Categoría: Lógica matemática
Wikimedia foundation. 2010.
