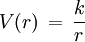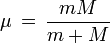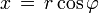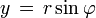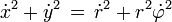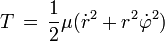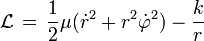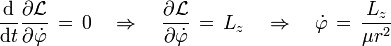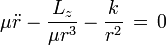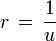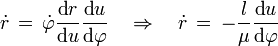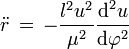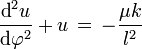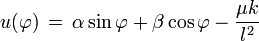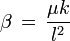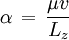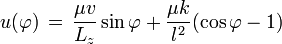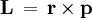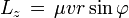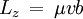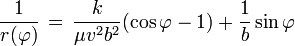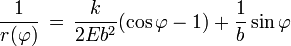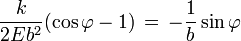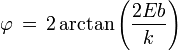- Dispersión en campo central
-
Dispersión en campo central
La dispersión en un campo central se refiere al cambio de cantidad de movimiento que sufren dos partículas al interaccionar por medio de un campo central, entendiendose por campo central, un campo de fuerza con simetría esférica. Para generalizar la solución a los campos centrales más comunes que se estudian en física elemental, vamos a trabajar con un campo cuyo potencial tiene una estructura general, que se puede representar matemáticamente según
un ejemplo clásico de campos de este tipo es el campo gravitacional. De importancia fundamental en la física.
Contenido
El Lagrangiano
En primer lugar será necesario aclarar, que es conveniente, y de hecho es la única forma de hacerlo! considerar como origen del sistema de coordenadas, el centro geométrico de la particula de mayor masa y desde allí estudiar el problema de un solo cuerpo que se mueve en torno al que está en el origen. Para hacer ésto, debemos tomar como masa de la segunda partícula la siguiente
ésta expresión es conocida como la masa reducida, y su obtención es simple, sin embargo no es el objetivo de éste artículo por lo cual se omite. Ahora debemos escribir la posición de la partícula de masa m en coordenadas polares, como se puede observar en la figura
notese que tanto r como θ son dependientes del tiempo, entonces si procedemos ahora a encontrar las velocidades obtendremos sin mucho esfuerzo
de aquí la energía cinética es simple y es
y utilizando el potencial propuesto en la sección anterior tendremos que el Lagrangiano es
que es el lagrangiano del sistema.
Ecuaciones de Movimiento
En la sección anterior obtuvimos el lagrangiano del sistema y es
de inmediato observamos que existe una cantidad conservada, es decir una constante del movimiento, para aclararlo a quien no esté familiarizado, si el lagrangiano no depende de una coordenada explícitamente, el momento conjugado a esa coordenada se conserva. Dicha cantidad es obviamente el momento angular perpendicular al plano de movimiento, es decir Lz, en efecto según la ecuación de Euler-Lagrangede Euler-Lagrange, tendremos
donde Lz es una constante del movimiento, aplicando ahora la ecuación de Euler-Lagrange para r, y sustituyendo el valor de
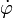 obtendremos
obtendremosésta ecuación es posible resolverla y encontrar la trayectoria de una partícula en un campo central, incluyendo por ejemplo, órbitas de sátelites y planetas. Para nuestro propósito, vamos a encontrar la trayectoria de dispersión de una partícula. Entonces procedamos a resolver, ésto es posible haciendo el cambio
aplicando la regla de la cadena se puede ver que
mediante el mismo procedimiento se puede verificar que
haciendo las sustituciones pertinentes obtendremos la siguiente ecuación
ésta es una ecuación diferencial lineal de segundo orden no homogénea, puede por sustitución verificar que la solución más general a la ecuación es
las constantes α y β se determinan evaluando las condiciones iniciales, en éste caso tenemos que para
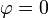 entonces puesto que la partícula viene desde el infinito tendremos
entonces puesto que la partícula viene desde el infinito tendremos 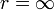 y claramente u(0) = 0 de donde se obtiene
y claramente u(0) = 0 de donde se obtienela segunda condición inicial, es que
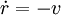 el signo negativo se debe a que la partícula viene desde la izquierda,
el signo negativo se debe a que la partícula viene desde la izquierda, 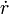 había sido determinado anteriormente por lo que es suficiente con sustituirla en la expresión y derivar
había sido determinado anteriormente por lo que es suficiente con sustituirla en la expresión y derivar 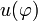 con respecto a
con respecto a 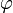 entonce se obtiene la constante α y es
entonce se obtiene la constante α y esasí que encontramos
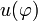 escrita explícitamente y es
escrita explícitamente y esÁngulo de dispersión
Sabemos que el momento angular viene dado por
y su módulo, en nuestro caso será
pero de la figura de la sección anterior es claro que
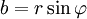 entonces se tiene
entonces se tienehaciendo la sustitución correcta en la ecuación de
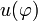 obtendremos
obtendremospero podemos observar que μv2 = 2T con T la energía cinética, que es la energía total inicialmente, y como obviamente se ha conservado la energía, es la energía total del sistema por ello escribiremos
el ángulo de dispersión será aquel para el cual
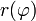 se aleja hacia el infinito por la derecha, en esas condiciones es obvio que se tendrá
se aleja hacia el infinito por la derecha, en esas condiciones es obvio que se tendráutilizando algunas identidades trigonométricas podemos encontrar que
es importante mencionar que la cantidad b es denominada parámetro de impacto y recordar que k es una constante que determina la forma específica del potencial V(r).
Referencia
- Landau, L.D.; Lifshitz E.M. (1991). «III», Reverté (ed.). Mecánica, 2ª edición, pp. 35-41. ISBN 84-291-4080-6.
- Eisberg, Robert; Resnick (1985). «4», Wiley (ed.). Fisica Cuantica, 2ª edición, pp. 90-95. ISBN 0-471-87373-X.
Categoría: Física
Wikimedia foundation. 2010.