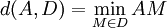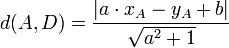- Distancia de un punto a una recta
-
Distancia de un punto a una recta
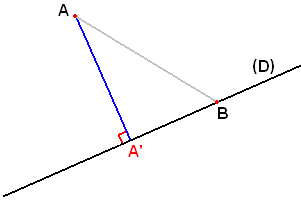
Sean A un punto y D una recta.
Se define la distancia entre A y D como la distancia mínima entre A y un punto M de D.- Para recta definida por su ecuación reducida
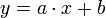
Obsérvese que
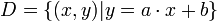
Demostración
Es fácil comprobar que este mínimo se realiza en el proyectado ortogonal de A sobre D, es decir el punto A' de la recta (D) tal que (AA') sea perpendicular a ella. En efecto, si se toma otro punto cualquiera B de (D), entonces en el triángulo rectángulo AA'B, la hipotenusa AB es más larga que el cateto AA'. Geométricamente se construye el proyectado A' deslizando una escuadra sobre una regla que sigue la recta D hasta encontrar el punto A; luego se mide la longitud AA'.
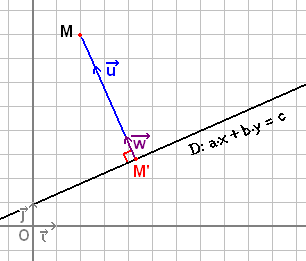
Un objetivo más ambicioso es el de encontrar una manera de calcular esta distancia, es decir sin pasar por una medición gráfica, forzosamente aproximativa. Para ello, es aconsejable utilizar un sistema de coordenadas ortonormal -
 en la figura. La recta y el punto cuya distancia se quiere medir son definidos por su ecuación cartesiana y sus coordenadas respectivamente:
en la figura. La recta y el punto cuya distancia se quiere medir son definidos por su ecuación cartesiana y sus coordenadas respectivamente: 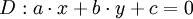 ; y
; y 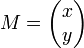
Si en la ecuación de la recta D variamos sólo el valor del parámetro "c" obtendremos una familia de rectas paralelas. De manera que para determinar un vector perpendicular podemos tomar c = 0. Así, los vectores sobre la recta tendrán la forma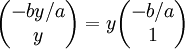 , que puede simplificarse a
, que puede simplificarse a 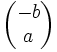
Busquemos un vector normal a
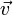 (es decir, perpendicular a la recta), que deberá cumplir que el producto escalar
(es decir, perpendicular a la recta), que deberá cumplir que el producto escalar 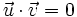 , y resulta ser
, y resulta ser 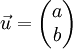 (de ahí el interés de la ecuación cartesiana) y al dividirlo por su norma se obtiene el vector normado
(de ahí el interés de la ecuación cartesiana) y al dividirlo por su norma se obtiene el vector normado 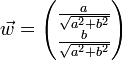 que define una medida algebraica sobre la recta (M'M):
que define una medida algebraica sobre la recta (M'M): 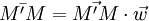
La distancia MM' es el valor absoluto de la medida algebraica:
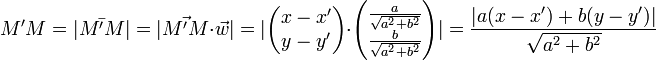
Como M' pertenece a D, sus coordenadas verifican a·x' + b·y' = -c luego lo anterior se simplifica así: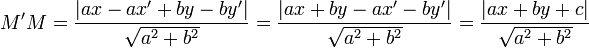
En conclusión: La distancia entre M y (D) es:
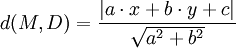
Esta fórmula es muy fácil de recordar: Se divide la expresión de la recta por la norma del vector y se pone el valor absoluto porque una distancia es siempre positiva.
- En el caso que la recta sea dada por el ángulo (θ) que hace con el eje de las abscisas y su ordenada al origen (b), la fórmula se simplifica:
- D: y = (tan θ) ·x + b se pone en forma cartesiana: (sin θ)·x - (cos θ)·y + b·cos θ = 0, luego, sabiendo que el vector
 es unitario:
es unitario: -
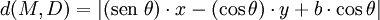
- Ejemplo: la primera diagonal del sistema de referencia corresponde a un ángulo
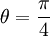 y b = 0. Como
y b = 0. Como 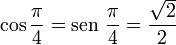 , se obtiene:
, se obtiene: 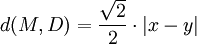
- En el caso de una recta definida por su ecuación reducida y = a·x + b; la ecuación cartesiana es a·x - y + b = 0 y la distancia a ella es:
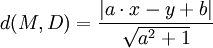
- Ejemplo: Tomando a = 1 y b = 0, se obtiene de nuevo el resultado del ejemplo anterior.
Se calcula de la misma manera la distancia de un punto y un plano en el espacio tridimensional: Si la ecuación del plano es
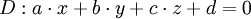 ; y el punto es
; y el punto es 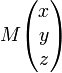 entonces:
entonces: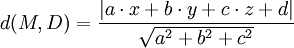
Lo anterior se generaliza a los espacios de dimensión finita n, y la distancia entre un punto y un hiperplano (subespacio de dimensión n-1), añadiendo cuantas variables hagan falta.
- El contenido de este artículo incorpora material de una entrada de la Enciclopedia Libre Universal, publicada en español bajo la licencia Creative Commons Compartir-Igual 3.0.
Categoría: Geometría -
Wikimedia foundation. 2010.