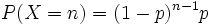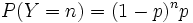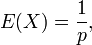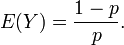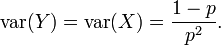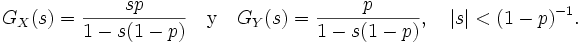- Distribución geométrica
-
Distribución geométrica
En teoría de probabilidad y estadística, la distribución geométrica es cualquiera de las dos distribuciones de probabilidad discretas siguientes:
- la distribución de probabilidad del número X del ensayo de Bernoulli necesaria para obtener un éxito, contenido en el conjunto { 1, 2, 3,...} o
- la distribución de probabilidad del número Y = X − 1 de fallos antes del primer éxito, contenido en el conjunto { 0, 1, 2, 3,... }.
Cual de éstas es la que uno llama "la" distribución geométrica, es una cuestión de convención y conveniencia.
Propiedades
Si la probabilidad de éxito en cada ensayo es p, entonces la probabilidad de que n ensayos sean necesarios para obtener un éxito es
para n = 1, 2, 3,.... Equivalentemente, la probabilidad de que haya n fallos antes del primer éxito es
para n = 0,1, 2, 3,....
En ambos casos, la secuencia de probabilidades es una progresión geométrica.
El valor esperado de una variable aleatoria X distribuida geométricamente es
y dado que Y = X-1,
En ambos casos, la varianza es
Las funciones generatrices de probabilidad de X y la de Y son, respectivamente,
Como su análoga continua, la distribución exponencial, la distribución geométrica carece de memoria. Esto significa que si intentamos repetir el experimento hasta el primer éxito, entonces, dado que el primer éxito todavía no ha ocurrido, la distribución de probabilidad condicional del número de ensayos adicionales no depende de cuantos fallos se hayan observado. El dado o la moneda que uno lanza no tiene "memoria" de estos fallos. La distribución geométrica es de hecho la única distribución discreta sin memoria.
De todas estas distribuciones de probabilidad contenidas en {1, 2, 3,... } con un valor esperado dado μ, la distribución geométrica X con parámetro p = 1/μ es la de mayor entropía.
La distribución geométrica del número y de fallos antes del primer éxito es infinitamente divisible, esto es, para cualquier entero positivo n, existen variables aleatorias independientes Y 1,..., Yn distribuidas idénticamente la suma de las cuales tiene la misma distribución que tiene Y. Estas no serán geométricamente distribuidas a menos que n = 1.
Distribuciones relacionadas
La distribución geométrica es un caso especial de la distribución binomial negativa con parámetro k = 1. Más generalmente, si Y 1,...,Yk son variables independientes distribuidas geométricamente con parámetro p, entonces
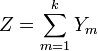 sigue a una distribución binomial negativa con parámetros k y p.
sigue a una distribución binomial negativa con parámetros k y p.Si Y1,...,Yr son variables independientes distribuidas geométricamente (con diferentes parámetros de éxito pm posibles ), entonces su mínimo W = minmYm es también geométricamente distribuido, con parámetro
p = 1 − ∏ (1 − pm) m .
Enlaces externos
- Geometric distribution en MathWorld (en inglés).
Categoría: Distribuciones discretas
Wikimedia foundation. 2010.