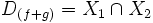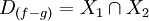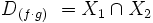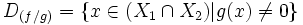- Dominio de definición
-
Dominio de definición
En matemáticas, el dominio (conjunto de definición o conjunto de partida) de una función
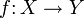 es el conjunto de existencia de ella misma, es decir, los valores para los cuales la función está definida. Es el conjunto de todos los objetos que puede transformar, se denota
es el conjunto de existencia de ella misma, es decir, los valores para los cuales la función está definida. Es el conjunto de todos los objetos que puede transformar, se denota 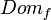 o bien
o bien 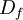 y está definido por:
y está definido por: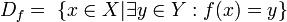
Contenido
Propiedades
Dadas dos funciones reales:
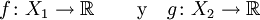
Se tienen las siguientes propiedades:
Ejemplos
Algunos dominios de funciones reales de variable real:
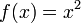 El dominio de esta función es
El dominio de esta función es 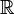
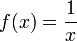 El dominio de esta función es
El dominio de esta función es 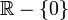 puesto que la función no está definida para x = 0.
puesto que la función no está definida para x = 0.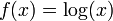 El dominio de esta función es
El dominio de esta función es 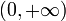 ya que los logaritmos están definidos sólo para números positivos.
ya que los logaritmos están definidos sólo para números positivos.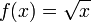 El dominio de esta función es
El dominio de esta función es 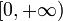 porque la raíz de un número negativo no existe en el campo de los Reales.
porque la raíz de un número negativo no existe en el campo de los Reales.Cálculo del dominio de una función
Para el cálculo certero del dominio de una función, debemos introducir el concepto de restricción en el campo real. Estas restricciones nos ayudarán a identificar la existencia del dominio de una función. Las más usadas son:
Raíz enésima de f(x)
No existe restricción si n es impar, pero si "n" es par, la función f(x) necesariamente deberá ser mayor no estricto de cero, ya que las raíces negativas no están definidas en el campo real. Por ejemplo:
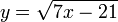
El índice de la raíz es par (2), por tanto
7x − 21 > = 0 despejando tenemos que
x>=3 El dominio entonces será el conjunto de todos los reales en el intervalo [3,∞+)
Logaritmo de f(x)
La restricción está al estudiar las propiedades de los logaritmos las cuales nos dicen que estos no están definidos para números negativos, por tanto toda función contenida dentro de un logaritmo es necesariamente mayor estricto de cero. Por ejemplo:
log(x2 − 9) Por la propiedad anteriormente citada tenemos que para que esta función exista, necesariamente
x2 − 9 > 0 despejando obtendremos dos soluciones x > 3 y x < − 3. La unión de ambas soluciones representa el dominio de la función, que está definida como el conjunto (-∞, -3) U (3, ∞+).
Fracciones
Véase también: División por ceroOtras propiedades de las matemáticas nos pueden ayudar a obtener el dominio de una función y excluir puntos donde esta no está definida, por ejemplo, una función que tenga forma de fracción no estará definida cuando el denominador valga cero, ya que esto es una indeterminación que daría una tendencia al infinito. Veamos
la función
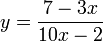 no estará definida cuando 10x − 2 = 0, despejando x = 1 / 5, es decir la variable x debe tener un valor diferente para poder existir, ya que en ese punto no está definida, por tanto el dominio de esta función será el conjunto de todos los reales menos ese punto. Su notación será R-{(1/5)}, que se lee, el conjunto de todos los reales menos el punto 0,20.
no estará definida cuando 10x − 2 = 0, despejando x = 1 / 5, es decir la variable x debe tener un valor diferente para poder existir, ya que en ese punto no está definida, por tanto el dominio de esta función será el conjunto de todos los reales menos ese punto. Su notación será R-{(1/5)}, que se lee, el conjunto de todos los reales menos el punto 0,20.El grado de dificultad se incrementa cuando buscamos el dominio de una función con variable en el denominador contenida dentro de un radical de índice par o logaritmo, ya que esto nos traslada a resolver una desigualdad. No obstante, el método de polos y ceros nos permite resolver esta clase de inecuaciones con facilidad.
Ejemplo
Para evidenciar este caso veamos este problema. Hallar el dominio de la siguiente función:
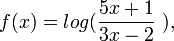
Para que esta función exista, necesariamente
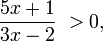
ya que no existe logaritmo de expresiones negativas. La solución de esta desigualdad, es explicada paso por paso en el artículo polos y ceros anteriormente citado, su solución constituirá el dominio de la función que en este caso será:
solución: (-∞, -1/5) U (2/3, ∞+)
Véase también
Categoría: Funciones
Wikimedia foundation. 2010.