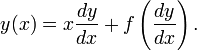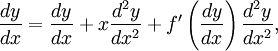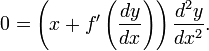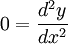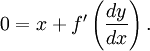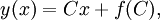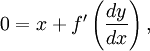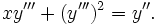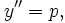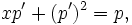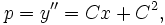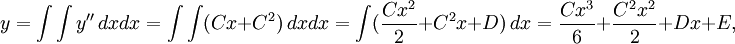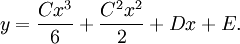- Ecuación diferencial de Clairaut
-
Ecuación diferencial de Clairaut
La ecuación diferencial de Clairaut, así llamada en honor a su inventor, el físico francés Alexis-Claude Clairaut, es una ecuación diferencial ordinaria de la forma:
Para resolver la ecuación, diferenciamos respecto a x, quedando:
por tanto
y así:
ó
En el primer caso, C = dy/dx para cualquier constante arbitraria C. Sustituyéndolo en la ecuación de Clairaut, tenemos la familia de ecuaciones dadas por
llamadas soluciones generales de la ecuación de Clairaut.
El otro caso,
define sólo una solución y(x), llamada solución singular, cuyo gráfico es envolvente de las gráficas de las soluciones generales. La solución singular se representa normalmente usando notación paramétrica, como: (x(p), y(p)), donde p representa dy/dx.
Ejemplo:Resolver:
Hacemos
por tanto
obteniendo la ecuación de Clairaut, cuya solución es
de la cual podemos obtener y integrando dos veces, así
siendo D y E otras dos constantes cualquiera.
Solución:
Categoría: Ecuaciones diferenciales ordinarias
Wikimedia foundation. 2010.