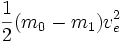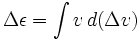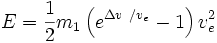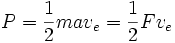- Ecuación del cohete de Tsiolskovski
-
Ecuación del cohete de Tsiolskovski
La ecuación del cohete de Tsiolkovski, llamada así por Konstantín Tsiolkovski que fue el primero que la derivó, considera el principio del cohete: un aparato que puede aplicar aceleración al mismo (empuje) expulsando parte de su masa a alta velocidad en la dirección opuesta, debido a la conservación de la cantidad de movimiento.
Contenido
Introducción
La expresión de Tsiolkovski expresa que para cualquier maniobra o viaje que incluya maniobras:
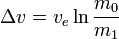
o equivalentemente

Donde:
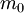 es la masa total inicial.
es la masa total inicial.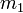 la masa total final
la masa total final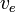 la velocidad de los gases de salida con respecto al cohete (impulso específico).
la velocidad de los gases de salida con respecto al cohete (impulso específico).
Por otro lado el término:
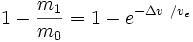 , es la fracción de masa (la parte de la masa total inicial que se utiliza para propulsar el cohete).
, es la fracción de masa (la parte de la masa total inicial que se utiliza para propulsar el cohete).
Δv (delta-v) es el resultado de integrar en el tiempo la aceleración producida por el uso del motor del cohete (no la aceleración debida a otras fuentes como rozamiento o gravedad). En el caso típico de aceleración en el sentido de la velocidad, es el incremento de la velocidad. En el caso de aceleración en el sentido contrario (desaceleración) es el decremento de la velocidad. La gravedad y el rozamiento cambian también la velocidad pero no forman parte de delta-v. Por ello, delta-v no es simplemente el cambio en la velocidad. Sin embargo, el empuje se aplica en corto tiempo, y durante ese periodo las otras fuentes de aceleración pueden ser negligibles, así que la delta-v de un momento determinado puede aproximarse al cambio de velocidad. La delta-v total puede ser simplemente añadida, aunque entre momentos de propulsión la magnitud y cantidad de velocidad cambia debido a la gravedad, como por ejemplo en una órbita elíptica.
La ecuación se obtiene integrando la ecuación de conservación del momento lineal.
- mdv = vedm
para un cohete simple que emite masa a velocidad constante (dm es la masa que se emite).
Aunque es una simplificación extrema, la ecuación del cohete muestra lo esencial de la física del vuelo del cohete en una única y corta ecuación. La magnitud delta-v es una de las cantidades más importantes en mecánica orbital que cuantifica lo difícil que es cambiar de una trayectoria a otra.
Claramente, para conseguir un delta-v elevada, debe ser m0 elevada (crece exponencialmente con delta-v), o m1 debe ser pequeña, o v debe ser elevada, o una combinación de éstos.
En la práctica, esto se consigue con cohetes muy grandes (aumentando m0), con varias fases (decrementando m1), y cohetes con combustibles con velocidades de escape muy elevadas. Los cohetes Saturno V utilizados en el Proyecto Apollo y los motores de iones usados en sondas no tripuladas de larga distancia son un buen ejemplo de esto.
La ecuación del cohete muestra un "decaimiento exponencial" de masa, pero no como función del tiempo, si no conforme a mientras se produce la delta-v. La delta-v que corresponde a la "vida media" es
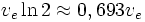
Fases
En el caso de cohetes de varias fases, la ecuación se aplica a cada fase, y en cada fase la masa inicial del cohete es la masa total del cohete después de dejar la fase anterior y la masa final es la del cohete justo antes de dejar la fase que se está calculando. El impulso específico para cada fase puede ser diferente.
Por ejemplo, si el 80% de la masa es el combustible de la primera fase y el 10% es masa en vacío de la primera fase y el 10% es el resto del cohete, entonces
- Δv = veln5 = 1,61ve
Con tres fases similares más pequeñas, se tiene
- Δv = 3veln5 = 4,83ve
y la carga de pago es un 0,1% de la masa inicial.
Un cohete de una fase a órbita, también con un 0,1% de carga de pago puede tener una masa del 11% para depósitos y motores y el 88,9% de combustible. Esto da
- Δv = veln(100 / 11,1) = 2,20ve
Si el motor de una nueva fase se enciende antes de que la fase anterior haya caído y los motores que trabajan simultáneamente tienen un impulso específico diferente (como es muchas veces el caso en cohetes de combustible sólido y fases líquidas), la situación es más complicada.
Energía
En el caso ideal m1 es la carga útil y m0 − m1 es la masa que reacciona (que corresponde a depósitos vacíos sin masa, etc.). La energía necesaria es
Ésta es la energía cinética de la masa de reacción y no la energía cinética requerida por la carga, pero si ve=10 km/s y la velocidad del cohete es 3 km/s, entonces la velocidad de la masa de reacción solo cambia desde 3 a 7 km/s; La energía "ahorrada" corresponde al incremento de la energía cinética específica (energía cinética por kg) para el cohete. En general:
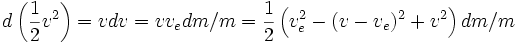
Se tiene
donde ε es la energía específica del cohete y Δv es una variable separada, no sólo el cambio en v. En el caso de usar el cohete parar decelerar, es decir, expeler masa de reacción en la dirección de la velocidad, v es negativa.
La fórmula es para el caso ideal sin pérdidas de energía por calor, etc. Esta última causa una reducción del empuje, así que es una desventaja aun cuando el objetivo es perder energía (decelererar).
Si la energía se produce por la masa misma, como en un cohete químico, el valor del combustible tiene que ser:
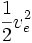 , donde para el valor del combustible se tiene que tomar también la masa del oxidante. Un valor típico es ve = 4,5km / s, correspondiente a 10,1 MJ/kg. La valor real es más alto pero parte de la energía se pierde en forma de calor que sale como radiación.
, donde para el valor del combustible se tiene que tomar también la masa del oxidante. Un valor típico es ve = 4,5km / s, correspondiente a 10,1 MJ/kg. La valor real es más alto pero parte de la energía se pierde en forma de calor que sale como radiación.La energía necesaria es
Conclusiones:
- Para
 se tiene
se tiene 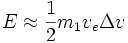
- Para una Δv dada, la energía mínima se necesita si ve = 0,6275Δv, requiriendo una energía de
- E = 0,772m1(Δv)2.
- Empezando desde velocidad cero es el 54,4 % más que la energía cinética de la carga de pago. Empezando desde una velocidad que no es cero, la energía requerida puede ser "menos" que el incremento de energía cinética de la carga. Éste puede ser el caso cuando la masa de reacción tiene una velocidad menor después de ser expelida que antes. Por ejemplo, desde una OBT de 300 km de altitud a una órbita de escape es un incremento de 29,8 MJ/kg, lo cual, usando un impulso específico de 4,5 km/s, tiene un coste neto de 20,6 MJ/kg (Δv = 3,20 km/s; las energías son por kg de carga de pago).
Esta optimización no tiene en cuenta las masa de los diferentes tipos de cohetes.
Además, para un objetivo determinado, como por ejemplo cambiar de una órbita a otra, la Δv requerida dependa mucho de la velocidad a la que el motos produce Δv y determinadas maniobras pueden ser imposibles si ésta es muy baja. Por ejemplo, un lanzamiento a OBT requiere normalmente una Δv de alrededor de 9,5 km/s (mayormente para conseguir la velocidad), pero si el motor pudiese producir Δv a una velocidad sólo algo más elevada que g, sería un lanzamiento lento y requeriría una Δv mucho más elevada (costaría una Δv de 9,8 m/s cada segundo). Si la aceleración posible es g o menor, no es posible ir a órbita con ese motor.
La potencia se obtiene de
donde F es el empuje y a es la aceleración debida a ella. Por ello, el empuje teórico posible por unidad de potencia es 2 dividido por el impulso específico en m/s. La eficiencia de empuje es el empuje real entre empuje teórico.
Si se usa energía solar se restringe a; en el caso de ve elevadas, la aceleración posible es inversamente proporcional a la velocidad de escape, así que el tiempo necesario para conseguir una delta-v es proporcional a ve; con el 100% de eficiencia:
- for
 we have
we have 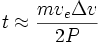
Ejemplos:
- potencia 1000 W, masa 100 kg, Δv= 5 km/s, ve= 16 km/s, lleva 1,5 meses.
- potencia 1000 W, masa 100 kg, Δv= 5 km/s, ve= 50 km/s, lleva 5 meses.
Por ello, la ve no puede ser demasiado alta.
Ejemplos
Se asume un impulso específico de 4,5 km/s y una Δv de 9,7 km/s (Tierra a OBT.
- Un cohete de una fase a órbita: 1 − e − 9,7 / 4,5 = 0,884, por ello el 88,4 % de la masa total inicial será propelente. El restante 11,6 % es para los motores, el tanque y la carga.
- Dos fases a órbita: se supone que la primera fase da una Δv de 5,0 km/s; 1 − e − 5,0 / 4,5 = 0,671, por ello, el 67,1%. El restante es el 32,9 %. Después de dejar la primera fase, la masa será este 32,9% menos el tanque y el motor de la priemra fase. Si se asume que esto es el 8% de la masa total inicial, queda el 24,9%. La segunda fase da una Δv de 4,7 km/s; 1 − e − 4,7 / 4,5 = 0,648, por ello, el 64,8% de la masa restante debe ser propelente, que es el 16,2 %, y el 8,7 % el tanque, el motor y la carga de la segunda fase, Así que hay disponible el 16,7 % para motores, tanques y carga de pago.
Véase también
- Propulsión (naves espaciales)
- Impulso específico
- Delta-v
- Masa de trabajo
Categorías: Astrodinámica | Cohetes
Wikimedia foundation. 2010.