- Elemento algebraico
-
Elemento algebraico
Un elemento algebraico sobre un cierto cuerpo matemático es un elmento de un conjunto que contiene a dicho cuerpo matemático y que constructible a partir de ciertas operaciones algebraicas relacionadas con los polinomios sobre el cuerpo original.
Contenido
Introducción
La Teoría de Cuerpos es una rama de la Teoría de Anillos, que a su vez es una rama del Álgebra Abstracta. Uno de las principales campos de estudio de la Teoría de Cuerpos es el de decidir si un polinomio cuyos coeficientes están en el cuerpo tiene sus raíces en el cuerpo (es decir, si al resolver la ecuación polinómica, las soluciones pertenecen o no al cuerpo).
Cuando un cuerpo está incluido en otro cuerpo puede ocurrir que los elementos del grande sean raíces de polinomios con coeficientes en el pequeño -en cuyo caso se dice que los elementos son algebraicos- o que haya elementos que no son raíces de ninguno de esos polinomios. En este último caso se dice que dichos elementos son trascendentes.
Construcción
(La siguiente información es de carácter técnico, y puede resultar ardua e incomprensible para el no iniciado en el Álgebra Abstracta, pero es esencial para comprender el desarrollo de esta rama de la Matemática. Por desgracia no puede exponerse de una manera más llana sin perder rigor, lo que haría que dejara de ser útil.)
Sean dos cuerpos
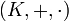 y
y 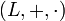 de forma que L es extensión de K. Sea
de forma que L es extensión de K. Sea 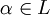 . Si
. Si 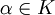 , entonces α es raíz del polinomio p(x) = x − α, que es irreducible en K[x] (todo polinomio de grado 1 es irreducible en cualquier anillo de polinomios). Si
, entonces α es raíz del polinomio p(x) = x − α, que es irreducible en K[x] (todo polinomio de grado 1 es irreducible en cualquier anillo de polinomios). Si 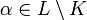 , entonces realizamos la siguiente construcción:
, entonces realizamos la siguiente construcción:- Construimos el conjunto
![K(\alpha):= \{\frac{f(\alpha)}{g(\alpha)}: f,g \in K[x]\}](/pictures/eswiki/51/33e02ad5b77544883db01c0838f01cca.png) . Este conjunto es un cuerpo, es extensión de K, es subcuerpo de L, y de hecho es la menor extensión de K que contiene a α. Se le denomina extensión generada por α sobre K.
. Este conjunto es un cuerpo, es extensión de K, es subcuerpo de L, y de hecho es la menor extensión de K que contiene a α. Se le denomina extensión generada por α sobre K.
- Construimos la aplicación
![\beta: K[x] \longrightarrow K(\alpha)](/pictures/eswiki/55/7bd19d0dbac123b4804a4627ef6bf8b0.png) que a cada polinomio
que a cada polinomio ![p(x) \in K[x]](/pictures/eswiki/98/b9db1f17d508db907f0a85c531f5be53.png) le hace corresponder su evaluación en α, i.e., β(p) = p(α). Esta aplicación es de hecho un isomorfismo de anillos conmutativos y unitarios, y se denomina aplicación evaluación.
le hace corresponder su evaluación en α, i.e., β(p) = p(α). Esta aplicación es de hecho un isomorfismo de anillos conmutativos y unitarios, y se denomina aplicación evaluación.
Ahora sólo pueden darse dos situaciones:
- Ker(β) = {0}. En este caso se dice que α es elemento trascendente sobre K.
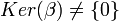 . Como K[x] es dominio de ideales principales y el núcleo de un homomorfismo de anillos es un ideal del anillo de partida del homomorfismo, entonces Ker(β) = (p) (esto es, el ideal generado por p) para algún
. Como K[x] es dominio de ideales principales y el núcleo de un homomorfismo de anillos es un ideal del anillo de partida del homomorfismo, entonces Ker(β) = (p) (esto es, el ideal generado por p) para algún ![p \in K[x]](/pictures/eswiki/51/36a6013b43f19ae5b9eaea971cbaee30.png) . Por el Primer Teorema de Isomorfía,
. Por el Primer Teorema de Isomorfía, 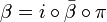 , donde
, donde 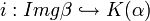 es el monomorfismo inclusión canónica (i.e., i(r) = r cualquiera que sea el
es el monomorfismo inclusión canónica (i.e., i(r) = r cualquiera que sea el 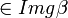 ),
), ![\pi: K[x] \longrightarrow \frac{K[x]}{Ker(\beta)}](/pictures/eswiki/99/c1990c2b742a207bec9fd48ff05085df.png) es el homomorfismo sobreyectivo aplicación proyección canónica (a cada
es el homomorfismo sobreyectivo aplicación proyección canónica (a cada ![p \in K[x]](/pictures/eswiki/51/36a6013b43f19ae5b9eaea971cbaee30.png) le asigna su clase
le asigna su clase 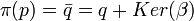 en el cociente
en el cociente ![\frac{K[x]}{Ker(\beta)}](/pictures/eswiki/52/4308c8ad8f2c3353340ae48e190da5c5.png) ), y
), y ![\bar{\beta}: \frac{K[x]}{(p)} = \frac{K[x]}{Ker(\beta)} \longrightarrow Img(\beta)](/pictures/eswiki/54/67ea1b599e892392aaf835c5bb892c69.png) es un isomorfismo de anillos unitarios.
es un isomorfismo de anillos unitarios.
- Como
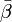 es sobreyectiva (ya que es isomorfismo),
es sobreyectiva (ya que es isomorfismo), 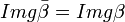 .
. ![Img \beta \cong \frac{K[x]}{(p)}](/pictures/eswiki/48/0cd13a888871a4042387056fe477fd58.png) (Primer Teorema de Isomorfía), que es subanillo de K(α), quien a su vez es un cuerpo, luego Imgβ es dominio íntegro por carecer de divisores de cero no nulos, con lo que también
(Primer Teorema de Isomorfía), que es subanillo de K(α), quien a su vez es un cuerpo, luego Imgβ es dominio íntegro por carecer de divisores de cero no nulos, con lo que también ![\frac{K[x]}{(p)}](/pictures/eswiki/55/76d36d16a17f33bf03d87767d734e4ce.png) es dominio íntegro.
es dominio íntegro.
- Pero si
![\frac{K[x]}{(p)}](/pictures/eswiki/55/76d36d16a17f33bf03d87767d734e4ce.png) es dominio íntegro será (p) ideal primo en K[x]. Sabemos que
es dominio íntegro será (p) ideal primo en K[x]. Sabemos que 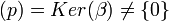 (por hipótesis), luego
(por hipótesis), luego 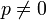 . Además, si fuera
. Además, si fuera ![p \notin K = U(K[x])](/pictures/eswiki/56/87aa879f089a09ed987b2c23e8cc06e2.png) (también por hipótesis). Con lo cual tenemos garantizado que p es un polinomio irreducible en K[x] (por ser dominio de ideales principales). Además, como K[x] es dominio de ideales principales, todo ideal primo es maximal, con lo cual (p) es ideal maximal de K[x], luego
(también por hipótesis). Con lo cual tenemos garantizado que p es un polinomio irreducible en K[x] (por ser dominio de ideales principales). Además, como K[x] es dominio de ideales principales, todo ideal primo es maximal, con lo cual (p) es ideal maximal de K[x], luego ![\frac{K[x]}{(p)}](/pictures/eswiki/55/76d36d16a17f33bf03d87767d734e4ce.png) es un cuerpo. Así
es un cuerpo. Así ![Img \beta \cong \frac{K[x]}{(p)}](/pictures/eswiki/48/0cd13a888871a4042387056fe477fd58.png) es un subcuerpo de K(α). Como
es un subcuerpo de K(α). Como ![K \subset K[x]](/pictures/eswiki/57/904b083a2317b1b9727762f920a09db1.png) , si
, si 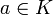 será
será 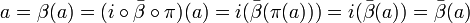 , con lo que se demuestra que K es subcuerpo de Imgβ.
, con lo que se demuestra que K es subcuerpo de Imgβ.
- Por otro lado,
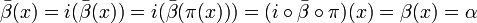 , con lo que
, con lo que ![\alpha \in Img \beta \cong \frac{K[x]}{(p)}](/pictures/eswiki/101/e7d259154029a8976cb357eef7fa2a1c.png) . Así, Imgβ es un subcuerpo de K(α) que contiene a K y a α. Como K(α) es la menor extensión de K que contiene a α llegamos a la conclusión de que
. Así, Imgβ es un subcuerpo de K(α) que contiene a K y a α. Como K(α) es la menor extensión de K que contiene a α llegamos a la conclusión de que ![K(\alpha) = Img \beta \cong \frac{K[x]}{(p)}](/pictures/eswiki/55/76851a0491b5c9732f2c2462ed74d225.png) .
.
En esta segunda situación (
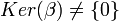 , o equivalentemente, existe algún
, o equivalentemente, existe algún ![p \in K[x]](/pictures/eswiki/51/36a6013b43f19ae5b9eaea971cbaee30.png) irreducible con
irreducible con ![\frac{K[x]}{(p)} \cong K(\alpha)](/pictures/eswiki/51/3c066aa6ba3755e1f2509be00db74462.png) ) se dice que α es algebraico sobre K.
) se dice que α es algebraico sobre K.Un elemento es algebraico sobre un cuerpo si y sólo si es raíz de algún polinomio a coeficientes en dicho cuerpo.
Polinomio mónico irreducible
Si α es un elemento algebraico sobre el cuerpo K de manera que
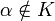 , el polinomio p que genera al núcleo de la aplicación evaluación (i.e., Kerβ = (p)) es irreducible. Dividiendo p por su coeficiente principal (aquél escalar que multiplica a la mayor potencia de la variable x) se obtiene un polinomio mónico (es decir, de manera que su coeficiente principal es la unidad), que se denota por
, el polinomio p que genera al núcleo de la aplicación evaluación (i.e., Kerβ = (p)) es irreducible. Dividiendo p por su coeficiente principal (aquél escalar que multiplica a la mayor potencia de la variable x) se obtiene un polinomio mónico (es decir, de manera que su coeficiente principal es la unidad), que se denota por 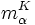 y se denomina polinomio mónico irreducible de α respecto de K.
y se denomina polinomio mónico irreducible de α respecto de K.Claramente,
![K(\alpha) \cong \frac{K[x]}{(m_{\alpha}^K)}](/pictures/eswiki/99/c4c97e044c1d6ab003ad65bd7e4137bc.png) .
.Véase también
- Elemento trascendente
- Número trascendente
- Número algebraico
- Extensión transcendente
- Extensión algebraica
Categoría: Teoría de cuerpos - Construimos el conjunto
Wikimedia foundation. 2010.
