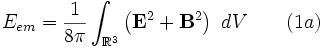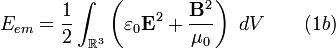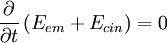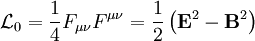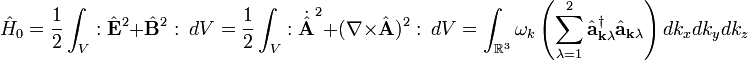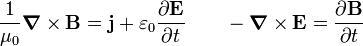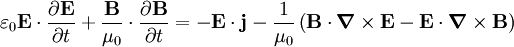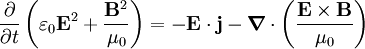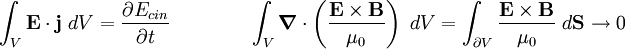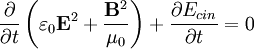- Energía electromagnética
-
Energía electromagnética
La energía electromagnética es la cantidad de energía almacenada en una región del espacio que podemos atribuir a la presencia de un campo electromagnético, y que se expresará en función de las intensidades de campo magnético y campo eléctrico. En un punto del espacio la densidad de energía electromagnética depende de una suma de dos términos proporcionales al cuadrado de las intensidades de campo.
Contenido
Energía electromagnética en física clásica
La energía contenida en un campo electromagético usando unidades c.g.s. viene dada por una suma de los cuadrados de los campos eléctrico y magnético:
En unidades del sistema internacional viene dado por:
Puede probarse que, cuando las aceleraciones de las cargas son muy pequeñas, la cantidad anterior sumada a la energía cinética de las cargas se conserva, es decir, se satisface la relación:
Por tanto si se define una cantidad llamada Etot = Ecin + Eem tenemos una ley de conservación de la energía en presencia de campos electromagnéticos.Radio clásico del electrón
En mecánica relativista masa y energía son "equivalentes". Eso implica que cualquier sistema físico con energía debería presentar una cierta inercia. Un intento original de explicar la masa del electrón fue suponer que éste podría ser pensado como una esfera de radio re sin masa fuera de la cual existía el campo eléctrico. Al tratar de mover el electrón este arrastraría a su campo eléctrico generando así una inercia, que sería vista como una masa efectiva. Asumiendo esas hipótesis la energía del campo eléctrico de un electrón medida por un observador en reposo respecto a él es:
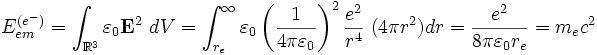
Despejando re de la ecuación anterior, obtenemos un valor estimado del radio del electrón llamado "radio clásico" del electrón e:
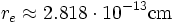
Energía de campos variables
Cuando un campo magnético es variable en una región del espacio desprovista de partículas cargadas este toma la forma de onda electromagnética. En ese caso la energía electromagnética puede calcularse a partir del cuadrado de la amplitud de esa onda electromagnética.
Este tipo de fenómeno es el que se da en las llamadas ondas electromagnéticas, como la luz, las ondas de radio y tv, las microondas, los rayos infrarrojos, los rayos ultravioleta, los rayos X o los rayos gamma de la radiactividad.
Energía electromagnética en mecánica cuántica
En teoría cuántica de campos postula que la energía de un estado del espacio-tiempo cuántico en el que existen campos eléctromagnéticos viene dada por un operador hamiltoniano que puede escribirse en términos de los operadores de campo cuánticos. La forma precisa del operador hamiltoniano se puede obtener a partir de la densidad lagrangiana clásica del campo.
Para un campo electromagnético la densidad lagrangiana viene dada en términos del tensor de campo electromagnético y de los campos eléctrico y magnético (en unidades cgs) por:
Cuantizando la anterior expresión mediante los procedimientos de cuantización canónica podemos obtener la expresión cuántica del operador hamiltoniano. En primer lugar es necesario escribir el tensor campo electromagnético en términos del potencial vector y entonces proceder a escribir el potencial vector en términos de operadores de creación y destrucción de fotones, ese resultado lleva integrando para sobre todos los posibles valores del momento del fotón y sumando para las dos helicidades posibles del fotón a la expresión cuántica para el operador hamiltoniano:
Donde la expresión dentro del sumatorio es precisamente el operador número que contabiliza el número de fotones con momento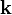 y helicidad λ. Se obtiene así el resultado de que la energía de campo electromagnético es proporcional al número de fotones y a la frecuencia de estos.
y helicidad λ. Se obtiene así el resultado de que la energía de campo electromagnético es proporcional al número de fotones y a la frecuencia de estos.Conservación de la energía
La interpretación de la cantidad anterior como energía del campo se debe a que la derivada temporal de la cantidad anterior es igual y opuesta a la energía cinética ganada por las cargas que se mueven en el campo:
Por tanto parece que si definimos la energía total como la suma de la energía cinética más una energía total asociada al campo obtenemos un nueva ley de la conservación de la energía en presencia de campos magnéticos. Para ver esto se parte de dos de las ecuaciones de Maxwell en el vacío:
Si se multiplica la primera escalarmente por el campo eléctrico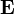 y la segunda por la inducción magnética
y la segunda por la inducción magnética 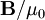 y sumamos las dos expresiones se llega a:
y sumamos las dos expresiones se llega a:
Y finalmente usando las propiedades de los operadores diferenciales vectoriales esto se puede reescribir como:
Integrando sobre un volumen finito que contenga al sistema de cargas que pretendemos estudiar, el primer miembro es la energía electromagnética dentro del volumen. El primer término del segundo miembro usando la expresión de la fuerza de Lorentz resulta ser la variación de la energía cinética de las cargas y el otro término es la integral de la divergencia del vector de Poynting que puede transformarse en una integral de superficie y si los campos caen a infinito más rápido que la 1/r y las dos expresiones son:
Así las cosas, si se toma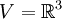 se tiene la siguiente expresión para la conservación de la energía en presencia de campos electromagnéticos:
se tiene la siguiente expresión para la conservación de la energía en presencia de campos electromagnéticos:
Relación que justifica el nombre de energía electromagnética.Categoría: Magnitudes electromagnéticas
Wikimedia foundation. 2010.