- Espacio de Hilbert equipado
-
Espacio de Hilbert equipado
En matemáticas, un espacio de Hilbert equipado (EHE) es una generalización de los espacios de Hilbert que permite ligar la teoría de distribuciones y los aspectos cuadrado-integrables del análisis funcional. Tales espacios fueron introducidos para estudiar la teoría espectral en sentido amplio y tienen amplia aplicación en mecánica cuántica.
Contenido
Motivación
Puesto que una función como:
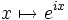
que es claramente un vector propio del operador diferencial:
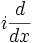
en la recta real
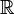 , no es de cuadrado integrable para la medida de Borel usual en
, no es de cuadrado integrable para la medida de Borel usual en 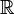 . Claramente la función exponencial compleja pertenece al espacio de vectorial complejo
. Claramente la función exponencial compleja pertenece al espacio de vectorial complejo 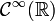 (que no es un espacio de Hilbert) pero no pertenece al espacio de Hilbert
(que no es un espacio de Hilbert) pero no pertenece al espacio de Hilbert 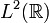 (asociado a la medida de Borel).
(asociado a la medida de Borel).Para poder definir propiedades de ortogonalidad a la función exponencial compleja del ejemplo anterior, se requiere un marco que exceda los límites estrictos de la teoría del espacio de Hilbert. Esto fue provisto por el aparato de distribuciones de Schwartz, y la teoría generalizada de la función propia fue desarrollada en los años 1950.
Introducción
El concepto del espacio equipado de Hilbert pone esta idea en marco funcional-analítico abstracto. Formalmente, un espacio equipado de Hilbert consiste en el espacio de Hilbert H, junto con un subespacio Φ que lleva una topología más fina, para la cual la inclusión natural:
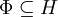
es continua. Se puede asumir que ese Φ es denso en H para la norma de Hilbert. Consideramos la inclusión del espacio dual H* en Φ*. El último, dual al Φ en su topología de la función de prueba, se realiza como un espacio de distribuciones o de funciones generalizadas de una cierta clase, y los funcionales lineales en el subespacio Φ del tipo:
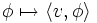
para v en H se representan fielmente como distribuciones (porque asumimos Φ denso). Ahora aplicando el teorema de representación de Riesz podemos identificar H* con H. Por lo tanto la definición del espacio equipado de Hilbert es en términos de un sandwich
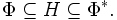
Definición formal
EHE en Mecánica cuántica
En mecánica cuántica el formalismo de espacios de Hilbert equipados permite tratar de un modo similar los estados ligados de partículas y estados libres. Un estado ligado corresponde normalmente a una situación donde una partícula tiene su movimiento restringido a una región finita del espacio, mientras que en un estado libre, más pertinentemente no-ligado, la partícula puede moverse por todo el espacio.
Un ejemplo físico aclara la situación. Si consideramos un átomo de hidrógeno los estados ligados corresponden a los electrones que orbitan alrededor del núcleo y no van mucho más allá del radio atómico, en este caso su energía mecánica total es negativa. Por otro lado un estado libre correspondería a la situación de un electrón con energía positiva se acerca al núcleo del átomo interactúa con él siendo desviado de su trayectoria pero tiene suficiente energía como para no ser capturado por el núcleo continuando así su camino lejos del átomo.
Desde un punto de vista matemático los estados ligados son vectores propios del Hamiltoniano (asociado a valores del espectro puntual del mismo). Por el contrario el espectro continuo del Hamiltoniano, que correspondería a estados libres carece de vectores propios propiamente dichos en un espacio de Hilbert convencional. Si se amplía el espacio de Hilbert convencional con ciertos vectores adicionales, entonces ciertos estados libres físicamente razonables pueden ser tratados como vectores propios generalizados correspondientes al espectro continuo.
Categoría: Análisis matemático
Wikimedia foundation. 2010.
