Fenómenos Ondulatorios: Oscilaciones Forzadas

Fenómenos Ondulatorios: Oscilaciones Forzadas

Saltar a navegación, búsqueda

Introduccion

Para entender la estrecha relacion que existe entre un fenomeno ondulatorio y un vibración forzada empezaremos definiendo un sistema que utilizaremos para generar una onda mecanica. Para ello se atara una cuerda ideal de longitud infinita de manera que el movimiento del sistema por definir, sirva como una fuente de ondas mecanicas.

Al hablar de una cuerda ideal nos referimos a una cuerda cuya masa es despreciable en comparacion con la del sistema. Estas hipotesis nos permitira igualar la coordenada de movimiento del sistema x con la de la cuerda ψ y sustituirla en su ecuacion de movimiento sin modificar la masa, el coeficiente de amortiguamiento ni su frecuencia natural ,esto es, resolver la ecuacion de movimiento del sistema equivaldra a tener una expresion para el movimiento que sigue la cuerda.

Una vez hecho esto realizaremos un analisis de forma grafica y analitica de dicha expresión

Deduccion del Modelo

Sea A un istema de masa m sujeto a un resorte ideal que obedece la ley de Hooke. Si el sistema se encuentra inmerso en un medio resistente que ejerce una fuerza de amortiguamiento proporcinal a la primera potencia de la velocidad y si además se ejerce sobre él una fuerza de la forma 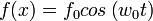$f(x)=f_{0}cos\left( w_{0}t\right)$ (véase Fig.1) entonces por segunda ley de Newton tenemos que: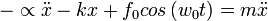

$-\propto\ddot{x}-kx+f_{0}cos\left( w_{0}t\right)=m\ddot{x}$

o bien

$m\ddot{x}+\propto\dot{x}+kx=f_{0}cos\left( w_{0}t\right)$

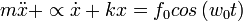
definiendo

$\beta\equiv\frac{\propto}{2m}, w\equiv\frac{k}{m}, F_{0}\equiv\frac{f_{0}}{m}$

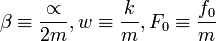
obtenemos la siguiente ecuacion diferencial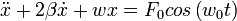

$\ddot{x}+2\beta\dot{x}+wx=F_{0}cos\left( w_{0}t\right)$

Ahora bien fijamos sobre el sistema una cuerda ideal de longitud l de manera que x = ψ obetenemos

$\ddot{\psi}+2\beta\dot{\psi}+w_{0}\psi=F_{0}cos\left( w_{0}t\right)$

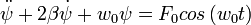
Cuya solucion es la suma de la ecuacion

ψ_general = ψ_homogenea + ψ_particular

Término Transitorio

Término Estable

---

$\ddot{\psi}_{c}+2\beta\dot{\psi}_{c}+w_{0}\psi_{c}=F_{c}$

$\psi_{c}=\psi_{0}e^{iw_{0}t}$

$\dot{\psi_{c}}=i\psi_{0}we^{iw_{0}t}$

$\ddot{\psi_{c}}=-\psi_{0}w^{2}e^{iw_{0}t}$

$(w_{0}^{2}-w^{2}+2\beta iw)\psi_{0}e^{iw_{0}t} = F_{c}$

$(w_{0}^{2}-w^{2}+2\beta iw)\psi_{c}= F_{c}$

$\psi_{c} = \frac{F_{0}e^{iwt}}{w_{0}^{2}-w^{2}+2\beta iw}$

$\psi_{c} \equiv \frac{F_{0}}{w_{0}^{2}-w^{2}+2\beta iw}$

$\psi_{c}=\frac{F_{0}}{w_{0}^{2}-w^{2}+2\beta iw}\frac{(w_{0}^{2}-w^{2}+2\beta iw)}{(w_{0}^{2}-w^{2}+2\beta iw)}=\frac{F_{0}(w_{0}^{2}-w^{2}+2\beta iw)}{(w_{0}^{2}-w^{2})^{2}+4\beta^{2}w^{2}}$

$\psi_{c}=\frac{F_{0}(w_{0}^{2}-w^{2})}{(w_{0}^{2}-w^{2})^{2}+4\beta^{2}w^{2}}-i\frac{F_{0}2\beta w}{(w_{0}^{2}-w^{2})^{2}+4\beta^{2}w^{2}}=\psi_{0}e^{i\propto}$

$\psi_{0}(w)=\frac{1}{\sqrt{(w_{0}^{2}-w^{2})^{2}+4\beta^{2}w^{2}}}$

$\propto(w)=ArcTan(\frac{-2\beta w}{w_{0}^{2}-w^{2}})$

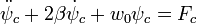
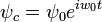
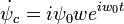
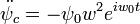
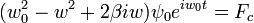
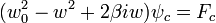
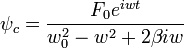
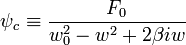
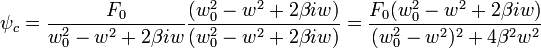
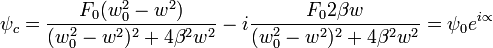
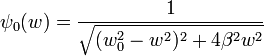
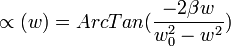
Análisis del Modelo

Obtenido de "Fen%C3%B3menos Ondulatorios: Oscilaciones Forzadas"