- Fibrado
-
Fibrado
En topología, un fibrado (o haz fibrado) es una función continua sobreyectiva π, de un espacio topológico E a otro espacio topológico B, satisfaciendo otra condición que lo hace de una forma particularmente simple localmente. Introduciendo otro espacio topológico F, utilizamos la función de proyección de B x F → B como modelo. Por ejemplo en el caso de un fibrado vectorial, F es un espacio vectorial sobre los números reales.
Contenido
Definición
Un fibrado consiste en una cuaterna
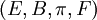 , donde
, donde 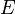 ,
, 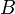 y
y 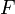 son variedades y
son variedades y 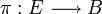 es una aplicación continua y sobreyectiva, de manera que se ha de cumplir que para cualquier
es una aplicación continua y sobreyectiva, de manera que se ha de cumplir que para cualquier 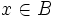 hay un entorno
hay un entorno 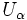 en
en 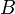 , tal que
, tal que 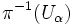 es homeomorfo a
es homeomorfo a 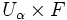 , de una manera tal que
, de una manera tal que 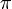 transporta a la proyección sobre el primer factor ( es decir, si
transporta a la proyección sobre el primer factor ( es decir, si 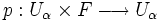 es la proyección sobre
es la proyección sobre 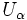 ; i.e.,
; i.e., 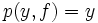 cualesquiera que sean
cualesquiera que sean 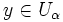 y
y 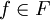 ). Además se exige que
). Además se exige que 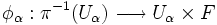 sea un homeomorfismo. Así
sea un homeomorfismo. Así 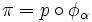 .
.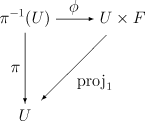
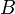 se llama el espacio de base del fibrado,
se llama el espacio de base del fibrado, 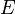 el espacio total, para cualquier
el espacio total, para cualquier 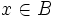 ,
, 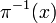 se llama la fibra en
se llama la fibra en 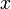 y la función
y la función 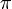 se llama la función de proyección.
se llama la función de proyección.Ejemplos
Cada función de proyección natural p: B x F → B es un fibrado. Los fibrados como éstos se llaman los fibrados triviales. Un ejemplo estándar, localmente trivial pero no (globalmente) trivial es la Banda de Möbius como E, en la cual B se puede tomar como un círculo y F un segmento de línea. La torcedura en la cinta es evidente sólo globalmente, mientras que localmente la estructura de la cinta define la topología. Cada fibrado vectorial es un fibrado; aquí F es un espacio vectorial sobre los números reales. Para calificar como fibrado vectorial, las transiciones que relacionan las vecindades localmente trivializables tendrán que ser lineales también. Cada espacio recubridor (en inglés covering space) es un fibrado; aquí el espacio fibra F es discreto.
Cada fibrado π : E → B es una función abierta, puesto que las proyecciones de productos cartesianos son funciones abiertas.
Secciones
Una sección de un fibrado es una función continua, f: B → E tal que π(f(x))=x, para x en B. Como los fibrados en general no tiene secciones, uno de los propósitos de la teoría es explicar su existencia. Esto conduce a la teoría de las clases características en topología algebraica.
Grupo estructural
Existe, a veces, un grupo topológico G de transformaciones de E, tal que si ρ denota la acción, π(ρ(g)[e])= π(e) para g en G y e en E. La condición indica que cada G-órbita reside dentro de una sola fibra. En ese caso, G se llama grupo estructural del fibrado. Para calificar como G-fibrado, las condiciones que emparejan entre las vecindades trivializable locales tendrían que ser los intertwiners de G-acciones también.
Si, además, actúa G libremente, transitivamente y continuamente sobre cada fibra, entonces llamamos al fibrado fibrado principal. Un ejemplo de un fibrado principal que ocurre naturalmente en geometría es el fibrado de todas las bases de los espacios tangentes a una variedad, con G grupo general lineal; la restricción en geometría de Riemann a las bases ortonormales, limitaría G al grupo ortogonal. Vea vierbein para más detalles.
Hacer G explícito es esencial para las operaciones de crear un fibrado asociado, y hacer precisa la reducción del grupo estructural de un fibrado.
Aplicaciones
Uno de los usos primarios de los fibrados está en las teorías de calibre.
Véase también
- Fibración
- Variedad
- Fibrado de Seifert
Enlaces externos
Categorías: Topología | Topología diferencial
Wikimedia foundation. 2010.
