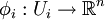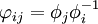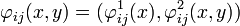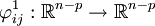- Foliación
-
Foliación
En matemáticas, una foliación es una partición en subvariedades diferenciables de otra variedad diferenciable (de tal modo que cada todas las subvariedades que conforman la foliación son de la misma dimensión m, siendo m menor menor que la dimensión de la variedad original).
Intuitivamente una foliación es como un conjunto de cortes o lonchas finas de la dimensión original en piezas de la misma dimensión. Por ejemplo se puede foliar espacio euclídeo tridimensional considerando que se trata de un apilamiento de infinitos planos euclídeos uno encima de otro. Cuando una variedad admite una foliación entonces localmente tiene una estructura topológica de variedad producto.
Contenido
Definición
Más formalmente, una foliación F de dimensión p o foliación p-dimensional de una variedad M es un recubrimiento topológico, formado por conjuntos Ui y equipado además con aplicaciones:
tal que en los solapes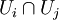 las funciones
las funciones 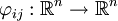 definidas mediante:
definidas mediante:
tienen la forma:
Donde x denota las primeras n − p coordenadas, y y denota las últimas p coordenadas. Es decir,
y
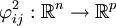 .
.
Ejemplos
Espacio euclídeo
Cubiertas
Si
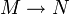 es una aplicación continua y exahustiva entre variedades y
es una aplicación continua y exahustiva entre variedades y 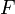 es una foliación sobre
es una foliación sobre 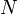 , entonces la aplicación anterior induce una foliación sobre
, entonces la aplicación anterior induce una foliación sobre 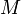 (pull-back de la aplicación anterior).
(pull-back de la aplicación anterior).Foliaciones e integrabilidad de campos n-formas
Véase también
- G-structura
- foliación de Reeb
- foliación de Taut
Categorías: Geometría diferencial | Topología diferencial
Wikimedia foundation. 2010.