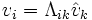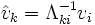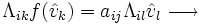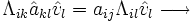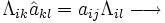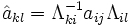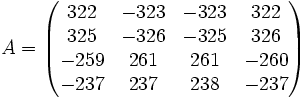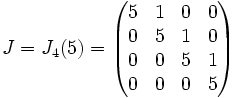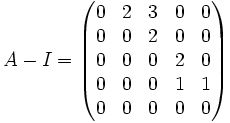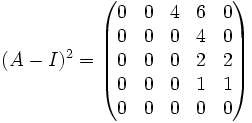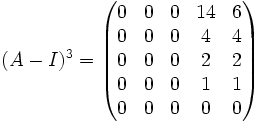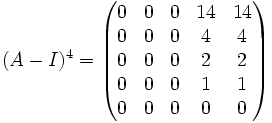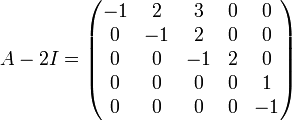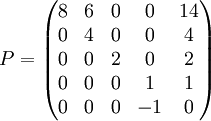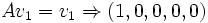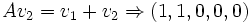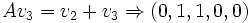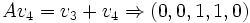Forma canónica de Jordan

Forma canónica de Jordan

Saltar a navegación, búsqueda

En álgebra lineal, la forma canónica de Jordan es la forma de la matriz de un endomorfismo de espacios vectoriales en cierta base asociada a la descomposición en suma directa de subespacios invariantes bajo dicho endomorfismo.

Definición

Recordemos que un endomorfismo es una aplicación lineal entre un mismo espacio vectorial 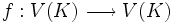$f:V(K)\longrightarrow V(K)$ (es decir tal que $f(\lambda x+\mu y)=\lambda f(x)+ \mu f(y), \forall\lambda\in K\land x,y\in V$).

Entre el espacio vectorial de los endomorfismos End(V) y el anillo de las matrices cuadradas existe un isomorfismo que, fijada una base en V(K), asigna una única matriz a cada endomorfismo (por supuesto si se cambia de base, la matriz también cambiará).

Supóngase que se tienen dos bases de V(K) llamadas 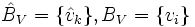$\hat B_{V}=\{\hat v_{k}\},B_{V}=\{v_{i}\}$ de modo que

$v_{i}=\Lambda_{ik}\hat v_{k}$

$\hat v_{k}=\Lambda_{ki}^{-1}v_{i}$

y sea a_ij y 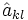$\hat a_{kl}$ las matrices asociadas al endomorfismo en las respectivas bases de modo que f(v_i) = a_ijv_j y 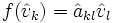$f(\hat v_{k})=\hat a_{kl}\hat v_{l}$, entonces las matrices se relacionan por

$f(v_{i})=a_{ij}v_{j}\longrightarrow$

$f(\Lambda_{ik}\hat v_{k})=a_{ij}\Lambda_{il}\hat v_{l}\longrightarrow$

$\Lambda_{ik}f(\hat v_{k})=a_{ij}\Lambda_{il}\hat v_{l}\longrightarrow$

$\Lambda_{ik}\hat a_{kl}\hat v_{l}=a_{ij}\Lambda_{il}\hat v_{l}\longrightarrow$

$\Lambda_{ik}\hat a_{kl}=a_{ij}\Lambda_{il}\longrightarrow$

$\hat a_{kl}=\Lambda_{ki}^{-1}a_{ij}\Lambda_{il}$

es decir hay una relación de similaridad entre ellas.

Un endomorfismo se dice diagonalizable por similaridad (o simplemente diagonalizable) si existe una base en la que su matriz asociada sea una matriz diagonal. Sin embargo la diagonalización no está asegurada, es decir no es posible decir que todo endomorfismo sea diagonalizable. La importancia de la diagonalización nos motiva a obtener una base en la que la matriz asociada a un endomorfismo no diagonalizable sea más simple aunque no diagonal. Para ello se seguirán las mismas técnicas que para diagonalización, usando la teoría sobre autovalores y autovectores (también llamados valores y vectores propios o en inglés eigenvalues y eigenvectors). Recordemos que dado un operador lineal 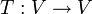$T:V\rightarrow V$ decimos que W subespacio de V es T-invariante si 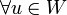$\forall u \in W$ se tiene que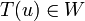 $T(u)\in W$

Motivación

Considérese la situación de una matriz diagonalizable. Una matriz cuadrada es diagonalizable si la suma de las dimensiones de los espacios propios (eigenspaces) es el número de filas o columnas de la matriz. Examinemos la matriz siguiente:

$A=\begin{pmatrix} 322 & -323 & -323 & 322 \\ 325 & -326 & -325 & 326 \\ -259 & 261 & 261 & -260 \\ -237 & 237 & 238 & -237 \end{pmatrix}$

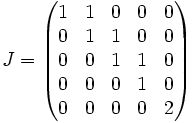
Tenemos valores propios de A que son sólo λ = 5, 5, 5, 5. Ahora bien, la dimensión del núcleo de A-5I es 1, por lo tanto A no es diagonalizable. Sin embargo, podemos construir la forma de Jordan de esta matriz. Dado que la dimensión es 1, sabemos que la forma de Jordan está compuesta de solo un bloque de Jordan, es decir, la forma de Jordan de A es:

$J=J_4(5)=\begin{pmatrix} 5 & 1 & 0 & 0 \\ 0 & 5 & 1 & 0 \\ 0 & 0 & 5 & 1 \\ 0 & 0 & 0 & 5 \end{pmatrix}$

Obsérvese que J puede escribirse como 5I+N, donde N es una matriz nilpotente. Puesto que ahora tenemos A similar a dicha matriz simple, podremos realizar cálculos que involucren a A usando la forma de Jordan, lo que en muchos casos puede simplificar el cálculo. Por ejemplo, calcular potencias de matrices es significativamente más sencillo usando la forma de Jordan.

Ejemplo

Hallar la forma canónica de Jordan de la matriz

$A=\begin{pmatrix} 1 & 2 & 3 & 0 & 0 \\ 0 & 1 & 2 & 0 & 0 \\ 0 & 0 & 1 & 2 & 0 \\ 0 & 0 & 0 & 2 & 1 \\ 0 & 0 & 0 & 0 & 1\end{pmatrix}$

Hallamos el polinomio característico:

P_A(λ) = (1 − λ)⁴(2 − λ)

Sus raíces son λ₁ = 1 y λ₂ = 2 con multiplicidades 4 y 1 respectivamente.

λ₁ = 1

Comencemos con λ₁, tenemos que hallar 4 vectores linealmente independientes, pues la multiplicidad de λ₁es 4. Pero no valen 4 vectores cualesquiera. Hay que hacer lo siguiente:

Hallar la cadena de kernels (A − λ₁I),(A − λ₁I)²,(A − λ₁I)³,...hasta que la dimensión del último sea la multiplicidad de la raíz (4 en este caso).

$A - I=\begin{pmatrix} 0 & 2 & 3 & 0 & 0 \\ 0 & 0 & 2 & 0 & 0 \\ 0 & 0 & 0 & 2 & 0 \\ 0 & 0 & 0 & 1 & 1 \\ 0 & 0 & 0 & 0 & 0\end{pmatrix}$

Ker(A − I) = < (1,0,0,0,0) > Luego dim(Ker(A − I)) = 1

$(A - I)^2=\begin{pmatrix} 0 & 0 & 4 & 6 & 0 \\ 0 & 0 & 0 & 4 & 0 \\ 0 & 0 & 0 & 2 & 2 \\ 0 & 0 & 0 & 1 & 1 \\ 0 & 0 & 0 & 0 & 0\end{pmatrix}$

Ker(A − I)² = < (1,0,0,0,0),(0,1,0,0,0) > Luego dim(Ker(A − I)²) = 2

$(A - I)^3=\begin{pmatrix} 0 & 0 & 0 & 14 & 6 \\ 0 & 0 & 0 & 4 & 4 \\ 0 & 0 & 0 & 2 & 2 \\ 0 & 0 & 0 & 1 & 1 \\ 0 & 0 & 0 & 0 & 0\end{pmatrix}$

Ker(A − I)³ = < (1,0,0,0,0),(0,1,0,0,0),(0,0,1,0,0) > Luego dim(Ker(A − I)³) = 3

$(A - I)^4=\begin{pmatrix} 0 & 0 & 0 & 14 & 14 \\ 0 & 0 & 0 & 4 & 4 \\ 0 & 0 & 0 & 2 & 2 \\ 0 & 0 & 0 & 1 & 1 \\ 0 & 0 & 0 & 0 & 0\end{pmatrix}$

Ker(A − I)⁴ = < (1,0,0,0,0),(0,1,0,0,0),(0,0,1,0,0),(0,0,0,1, − 1) > Luego dim(Ker(A − I)⁴) = 4

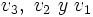Ya hemos llegado a la dimensión máxima. Ahora tomamos un vector $v_4 \in Ker(A-I)^4$ pero que no pertenezca a ninguno de los anteriores. Por ejemplo, v₄ = (0,0,0,1, − 1). Ahora hallar $v_3,~v_2~y~ v_1$ es muy fácil:

v₃ = (A − I)v₄ = (0,0,2,0,0)

v₂ = (A − I)²v₄ = (A − I)v₃ = (6,4,0,0,0)

v₁ = (A − I)³v₄ = (A − I)v₂ = (8,0,0,0,0)

λ₂ = 2

$A - 2I=\begin{pmatrix} -1 & 2 & 3 & 0 & 0 \\ 0 & -1 & 2 & 0 & 0 \\ 0 & 0 & -1 & 2 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & -1\end{pmatrix}$

Ker(A - 2I) = <(14,4,2,1,0)>. Ya tenemos los 5 vectores de la nueva base.

Matriz de cambio de base

$P=\begin{pmatrix} 8 & 6 & 0 & 0 & 14 \\ 0 & 4 & 0 & 0 & 4 \\ 0 & 0 & 2 & 0 & 2 \\ 0 & 0 & 0 & 1 & 1 \\ 0 & 0 & 0 & -1 & 0\end{pmatrix}$

Matriz Canónica de Jordan en la base P

Para hallar la matriz de Jordan sólo hay que hacer las imágenes por A, de los vectores de la base de Jordan, y expresarlos en dicha base:

$Av_1 = v_1 \Rightarrow (1,0,0,0,0)$

$Av_2 = v_1 + v_2 \Rightarrow (1,1,0,0,0)$

$Av_3 = v_2 + v_3 \Rightarrow (0,1,1,0,0)$

$Av_4 = v_3 + v_4 \Rightarrow (0,0,1,1,0)$

$Av_5 = 2v_5 \Rightarrow (0,0,0,0,2)$

$J=\begin{pmatrix} 1 & 1 & 0 & 0 & 0 \\ 0 & 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 2\end{pmatrix}$

Se cumple J = P ^{− 1}AP

Obtenido de "Forma can%C3%B3nica de Jordan"