Función unitaria de Heaviside
- Función unitaria de Heaviside
-
La función escalón de Heaviside, también llamada función escalón unitario, debe su nombre al matemático inglés Oliver Heaviside. Es una función discontinua cuyo valor es 0 para cualquier argumento negativo, y 1 para cualquier argumento positivo:

Tiene aplicaciones en ingeniería de control y procesamiento de señales, representando una señal que se enciende en un tiempo específico, y se queda prendida indefinidamente.
Propiedades
- Cambio de signo del argumento.



- Definición como límite de otras funciones.


- Es la integral de la función delta de Dirac.

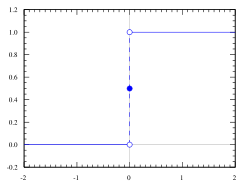
función escalón considerando
H(0) = 1/2.
El valor de H(0) es convencional. La mayoría de autores lo definen como H(0) = 1, otros H(0) = 0. Algunos que lo definen como H(0) = 1/2, ya que maximiza la simetría de la función, y permite una representación de la misma a través de la función signo:


Puede especificarse con un subíndice el valor que se va a usar para H(0), de la siguiente forma:

Una forma de representar esta función es a través de la integral

Véase también
Enlaces externos
Wikimedia foundation.
2010.
Mira otros diccionarios:
Función escalonada — Una función escalonada es aquella función definida a trozos que en cualquier intervalo finito [a, b] en que esté definida tiene un número finito de discontinuidades c1 < c2 < ... < cn, y en cada intervalo ]ck, ck+1[ es constante,… … Wikipedia Español
Función definida a trozos — En matemáticas, una función definida a trozos (también conocida como función por partes) es una función cuya definición (la regla que define la dependencia) cambia dependiendo del valor de la variable independiente. Matemáticamente, una función… … Wikipedia Español
Oliver Heaviside — hacia 1890 Nacimiento … Wikipedia Español
Anexo:Funciones matemáticas — Este artículo o sección necesita referencias que aparezcan en una publicación acreditada, como revistas especializadas, monografías, prensa diaria o páginas de Internet fidedignas. Puedes añadirlas así o avisar … Wikipedia Español
Funciones de parte entera — En matemática, las funciones de parte entera son aquellas funciones: que toman un número real y devuelven un número entero mayor o menor a ese número. Las funciones más conocidas son la función piso[1] y la función techo.[2] … Wikipedia Español
Transformada de Fourier — Para otros usos de este término, véase Transformación (desambiguación). En matemática, la transformada de Fourier es una aplicación que hace corresponder a una función f, con valores complejos y definida en la recta, con otra función g definida… … Wikipedia Español
Anexo:Derivadas — La operación fundamental en el cálculo diferencial es encontrar una derivada. Esta tabla enlista las derivadas de varias funciones. En lo sucesivo, f y g son funciones de x y c es una constante con respecto a x. Se presupone al conjunto de los… … Wikipedia Español












