Sobreaceleración

La sobreaceleración (conocida también como tirón o sacudida) es la tasa de cambio de la aceleración, es decir, la derivada de la aceleración con respecto a el tiempo, la segunda derivada de la velocidad, o la tercera derivada de la posición. Dado que la aceleración es una magnitud vectorial, la sobreaceleración también lo es.

$\vec {S}(t) = \frac {\mathrm{d} \vec a} {\mathrm{d}t} = \frac {\mathrm{d}^2 \vec v} {\mathrm{d}t^2} = \frac {\mathrm{d}^3 \vec r} {\mathrm{d}t^3}$

donde

$\vec a$ es la aceleración,

$\vec v$ es la velocidad,

$\vec r$ es la posición,

t es el tiempo.

Sistemas mecánicos

La gran mayoría de sistemas mecánicos para el movimiento de partículas o cuerpos están constituidos por ecuaciones diferenciales de segundo orden. Esto llevó a conjeturar que cualquier sistema fundamental debía estar descrito por ecuaciones diferenciales de como mucho segundo orden. Esto tiene sentido para el movimiento de partículas o cuerpos, donde esencialmente se pretende relacionar las fuerzas existentes con la trayectoria de la partícula. Puesto que la geometría diferencial de curvas prueba que una curva queda completamente determinada (salvo traslación y rotación) si se especifican en cada punto la curvatura y la torsión, y estas a su vez son completamente expresables en términos de las derivadas primera y segunda de las coordenadas, resulta que el movimiento de una partícula, conocida su posición y velocidad inicial, está completamente especificado si se relacionan las fuerzas con las derivadas primera y segunda.

Sin embargo otros sistemas físicos pueden exhibir conductas más complejas ya que en ellos se deben especificar ecuaciones para más parámetros que los que determinan una trayectoria continua en el espacio, y por tanto podrían requerir la especificación de derivadas terceras.

Aplicaciones

Sistemas de sobreaceleración

Un sistema de sobreaceleración es un sistema cuya evolución temporal viene dada por una ecuación del tipo (Sprott, 2003):

$\frac{\mathrm{d}^3 x}{\mathrm{d} t^3}= f\left(\frac{\mathrm{d}^2 x}{\mathrm{d} t^2},\frac{\mathrm{d} x}{\mathrm{d} t},x\right).$

Por ejemplo, ciertos circuitos electrónicos simples sólo pueden ser diseñados mediante el uso de ecuaciones que involucren sobreaceleraciones o ecuaciones diferenciales que involucren hasta la tercera derivada de alguna magnitud. Estos circuitos se conocen como circuitos de sacudida.

Una de las propiedades más interesantes de los sistemas de sobreaceleración es la frecuencia con la que exhiben comportamientos caóticos. De hecho ciertos, sistemas caóticos bien conocidos, como el atractor de Lorenz y el atractor de Rössler, se describen normalmente como sistemas de tres ecuaciones diferenciales de primer orden, que pueden ser combinadas de manera equivalente en una única ecuación más complicada de tercer orden. Un ejemplo de este tipo de sistemas sería:

$\frac{\mathrm{d}^3 x}{\mathrm{d} t^3}+A\frac{\mathrm{d}^2 x}{\mathrm{d} t^2}+\frac{\mathrm{d} x}{\mathrm{d} t}-|x|+1=0.$

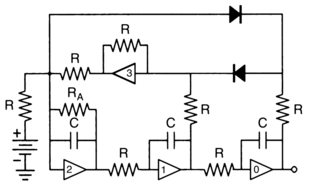
Donde A es un parámetro ajustable. Esta ecuación tiene una solución caótica para A=3/5 que puede ser reproducida mediante el siguiente circuito de sacudida:

En el circuito anterior, todas las resistencias son de igual valor, excepto R_A = R / A = 5R / 3, y todos los condensadores son de igual capacidad. La frecuencia dominante será 1 / 2πRC. La salida del Amplificador Operacional 0 corresponderá a la variable x, la salida 1 corresponderá a la primera derivada de x y la salida de 2 corresponderá a la segunda derivada.

Véase también

• Cinemática
• Tiempo
• Posición
• Velocidad
• Aceleración
• Derivada

Referencias

• Sprott JC (2003). Chaos and Time-Series Analysis. Oxford University Press. ISBN 0-19-850839-5.