Álgebra de Boole

Álgebra de Boole (también llamada Retículas booleanas) en informática y matemática, es una estructura algebraica que esquematiza las operaciones lógicas Y, O , NO y Si (AND,OR,NOT,IF), así como el conjunto de operaciones unión, intersección y complemento.

Se denomina así en honor a George Boole (2 de noviembre de 1815 a 8 de diciembre de 1864), matemático inglés que fue el primero en definirla como parte de un sistema lógico en el año 1854, en su tratado An investigation of the laws of thought on which to found the mathematical theories of logic and probabilities. El álgebra de Boole fue un intento de utilizar las técnicas algebraicas para tratar expresiones de la lógica proposicional. En la actualidad, el álgebra de Boole se aplica de forma generalizada en el ámbito del diseño electrónico. Claude Shannon fue el primero en aplicarla en el diseño de circuitos de conmutación eléctrica biestables, en 1948. Esta logica se puede aplicar a dos campos:

Al análisis, porque es una forma concreta de describir como funcionan los circuitos.
Al diseño, ya que teniendo una función aplicamos dicha álgebra, para poder desarrollar una implementación de la función.

Definición

Una álgebra de Boole es una tripleta $(\mathfrak{B},+,\cdot)$. Donde $\mathfrak{B}\neq\phi$, + y $\cdot$ son operaciones internas en $\mathfrak{B}$ y además para cualquier $x,y,z\in\mathfrak{B}$ se cumplen los siguientes axiomas:

1. Propiedad conmutativa:

$x + y = y + x \;$

$x \cdot y = y \cdot x$

2. Propiedad asociativa:

$x + (y + z) = (x + y) + z \;$

$x \cdot(y \cdot z) = (x \cdot y) \cdot z \;$

3. Propiedad distributiva:

$x + (y \cdot z) = (x + y) \cdot (x + z)$

$x \cdot( y + z) = (x \cdot y) + (x \cdot z)$

4. Propiedad de los neutros. Existen $0,1\in\mathfrak{B}$ tales que:

$x + 0 = x \;$

$x \cdot 1 = x \;$

5. Propiedad de los opuestos. Existe $\overline{x}\in\mathfrak{B}$ tal que:

$x \,$	$\overline{x}$	$x + \overline{x}$
0	1	1
1	0	1

$x + \overline{x} = 1$

$x \,$	$\overline{x}$	$x \cdot \overline{x}$
0	1	0
1	0	0

$x \cdot \overline{x} = 0$

Como retículo

Como retículo presenta las siguientes propiedades, las leyes principales son estas:

1. Ley de Idempotencia:

$a \cdot a = a \,$

$a + a = a \,$

2. Ley de Asociatividad:

$a \cdot (b \cdot c) = (a \cdot b ) \cdot c\,$

$a + (b + c) = (a + b ) + c \,$

3. Ley de Conmutatividad:

$a \cdot b = b \cdot a \,$

$a + b = b + a \,$

4. Ley de Cancelativo

$(a \cdot b) + a = a \,$

$(a + b) \cdot a = a \,$

Operaciones

Hemos definido el conjunto A = {1,0} como el conjunto universal sobre el que se aplica el álgebra de Boole, sobre estos elementos se definen varias operaciones, veamos las más fundamentales:

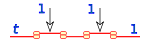
Operación suma

a	b	a + b
0	0	0
0	1	1
1	0	1
1	1	1

La operación suma (+) asigna a cada par de valores a, b de A un valor c de A:

$a + b = c \,$

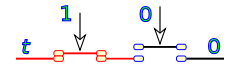
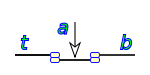
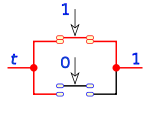
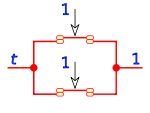
Su equivalencia en lógica de interruptores es un circuito de dos interruptores en paralelo.

Si uno de los valores de a o b es 1, el resultado será 1, es necesario que los dos sumandos sean 0, para que el resultado sea 0.

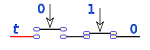
Operación producto

a	b	a $\cdot$ b
0	0	0
0	1	0
1	0	0
1	1	1

La operación producto ($\cdot$) asigna a cada par de valores a, b de A un valor c de A:

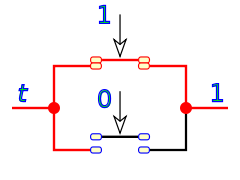
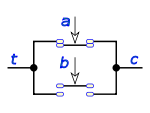
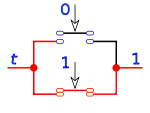
$a \cdot b = c$

Esta operación en lógica de interruptores es un circuito en serie de dos interruptores

solo si los dos valores a y b son 1, el resultado será 1, si uno solo de ellos es 0 el resultado será 0.

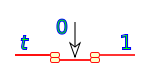
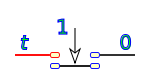
Operación negación

a	$\bar {a}$
0	1
1	0

La operación negación presenta el opuesto del valor de a:

$\bar {a} = b \,$

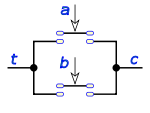
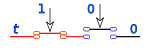
Un interruptor inverso equivale a esta operación:

Operaciones combinadas

a	b	$\bar {a}$	$\bar {a} + {b}$
0	0	1	1
0	1	1	1
1	0	0	0
1	1	0	1

Partiendo de estas tres operaciones elementales se pueden realizar otras más complejas, que podemos representar como ecuaciones booleanas, por ejemplo:

$\bar {a} + {b} = c \,$

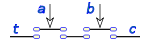
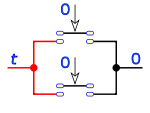
Que representado en lógica de interruptores es un circuito de dos interruptores en paralelo, siendo el primero de ellos inverso.

La distinta secuencia de valores de a y b da los resultados vistos en la tabla de verdad.

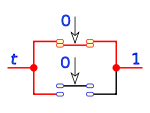
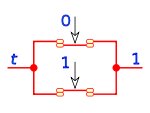
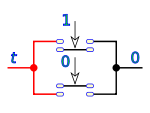
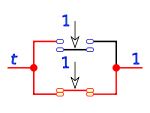
Leyes fundamentales

El resultado de aplicar cualquiera de las tres operaciones definidas a variables del sistema booleano resulta en otra variable del sistema, y este resultado es único.

1. Ley de idempotencia:

$a \cdot a = a \,$

$a + a = a \,$

2. Ley de involución:

$\overline {\bar {a}} = a$

3. Ley conmutativa:

$a \cdot b = b \cdot a \,$

$a + b = b + a \,$

4. Ley asociativa:

$a \cdot (b \cdot c) = (a \cdot b ) \cdot c\,$

$a + (b + c) = (a + b ) + c \,$

5. Ley distributiva:

$a \cdot (b + c) = (a \cdot b) + (a \cdot c) \,$

$(a + b ) \cdot c = (a \cdot c) + (b \cdot c) \,$

$a + (b \cdot c) = (a + b) \cdot (a + c) \,$

$(a \cdot b ) + c = (a + c) \cdot (b + c) \,$

$a + \bar {a} \cdot b = a + b \,$

6. Ley de cancelación:

$(a \cdot b) + a= a \,$

$(a + b) \cdot a= a \,$

7. Ley de identidad:

$a + 0 = a \,$

$a + 1 = 1 \,$

$a \cdot 1 = a \,$

$a \cdot 0 = 0 \,$

8. Leyes de De Morgan:

$\overline {(a + b)}= \bar {a} \cdot \bar {b} \,$

$\overline {(a \cdot b)} = \bar {a}+ \bar {b} \,$

Principio de dualidad

El concepto de dualidad permite formalizar este hecho: a toda relación o ley lógica le corresponderá su dual, formada mediante el intercambio de los operadores unión (suma lógica) con los de intersección (producto lógico), y de los 1 con los 0.

Además hay que cambiar cada variable por su negada. Esto causa confusión al aplicarlo en los teoremas básicos, pero es totalmente necesario para la correcta aplicación del principio de dualidad. Véase que esto no modifica la tabla adjunta.

	Adición	Producto
1	$a + \bar {a} = 1 \,$	$a \cdot \bar{a} = 0$
2	$a + 0 = a \,$	$a \cdot 1 = a \,$
3	$a + 1 = 1 \,$	$a \cdot 0 = 0 \,$
4	$a + a = a \,$	$a \cdot a = a \,$
5	$a + b= b+ a \,$	$a \cdot b = b \cdot a \,$
6	$a + (b + c) = (a + b) + c \,$	$a \cdot (b \cdot c) = (a \cdot b) \cdot c \,$
7	$a + ( b \cdot c ) = (a + b) \cdot (a + c) \,$	$a \cdot (b + c) = a \cdot b + a \cdot c \,$
8	$a + a \cdot b = a \,$	$a \cdot (a + b) = a \,$
9	$\overline {(a + b)} = \bar {a} \cdot \bar {b}$	$\overline {(a \cdot b)} = \bar {a} + \bar {b} \,$

Otras formas de notación del álgebra de Boole

En matemática se emplea la notación empleada hasta ahora ({0,1}, + , $\cdot$ ) siendo la forma más usual y la más cómoda de representar.

Por ejemplo las leyes de De Morgan se representan así:

$\overline {a + b}= \bar {a} \cdot \bar {b} \,$

$\overline {a \cdot b} = \bar {a}+ \bar {b} \,$

Cuando el álgebra de Boole se emplea en electrónica, suele emplearse la misma denominación que para las puerta lógica AND (Y), OR (O) y NOT (NO), ampliándose en ocasiones con X-OR (O exclusiva) y su negadas NAND (NO Y), NOR (NO O) y X-NOR (equivalencia). las variables pueden representarse con letras mayúsculas o minúsculas, y pueden tomar los valores {0, 1}

Empleando esta notación las leyes de De Morgan se representan:

$\mbox{NOT }(a \mbox{ OR } b)= \mbox{NOT } a \mbox{ AND } \mbox{NOT } b \,$

$\mbox{NOT }(a \mbox{ AND } b) = \mbox{NOT } a \mbox{ OR } \mbox{NOT } b \,$

En su aplicación a la lógica se emplea la notación $\land \lor \lnot$ y las variables pueden tomar los valores {F, V}, falso o verdadero, equivalentes a {0, 1}

Con la notación lógica las leyes de De Morgan serían así:

$\lnot {(a \lor b)}= \lnot {a} \land \lnot {b} \,$

$\lnot {(a \land b)} = \lnot {a} \lor \lnot {b} \,$

En el formato de Teoría de conjuntos el Álgebra de Boole toma el aspecto: $(\cup , \cap , \sim , \{0,1\} )$

En esta notación las leyes de De Morgan serían así:

$\sim {(a \cup b)} = \; \sim {a} \; \cap \sim {b} \,$

$\sim {(a \cap b)} = \; \sim {a} \; \cup \sim {b} \,$

Desde el punto de vista practico existe una forma simplificada de representar expresiones booleanas. Se emplean apóstrofos (') para indicar la negación, la operación suma (+) se representa de la forma normal en álgebra, y para el producto no se emplea ningún signo, las variables se representan, normalmente con una letra mayúscula, la sucesión de dos variables indica el producto entre ellas, no una variable nombrada con dos letras.

La representación de las leyes de De Morgan con este sistema quedaría así, con letra minúsculas para las variables:

$(a + b)' = a' b' \,$

$(a b)' = a' + b' \,$

y así, empleando letras mayúsculas para representar las variables:

$(A + B)' = A' B' \,$

$(A B)' = A' + B' \,$

Todas estas formas de representación son correctas, se utilizan de hecho, y pueden verse al consultar bibliografía. La utilización de una u otra notación no modifica el álgebra de Boole, solo su aspecto, y depende de la rama de las matemáticas o la tecnología en la que se esté utilizando para emplear una u otra notación.

Álgebra de Boole aplicada a la informática

Se dice que una variable tiene valor booleano cuando, en general, la variable contiene un 0 lógico o un 1 lógico. Esto, en la mayoría de los lenguajes de programación, se traduce en false (falso) o true (verdadero), respectivamente.

Una variable puede no ser de tipo booleano, y guardar valores que, en principio, no son booleanos; ya que, globalmente, los compiladores trabajan con esos otros valores, numéricos normalmente aunque también algunos permiten cambios desde, incluso, caracteres, finalizando en valor booleano.

El 0 lógico

El valor booleano de negación suele ser representado como false, aunque también permite y equivale al valor natural, entero y decimal (exacto) 0, así como la cadena "false", e incluso la cadena "0".

El 1 lógico

En cambio, el resto de valores apuntan al valor booleano de afirmación, representado normalmente como true, ya que, por definición, el valor 1 se tiene cuando no es 0. Cualquier número distinto de cero se comporta como un 1 lógico, y lo mismo sucede con casi cualquier cadena (menos la "false", en caso de ser ésta la correspondiente al 0 lógico).

Jerarquía de los operadores

Al evaluar una expresión booleana, deben realizarse las operaciones de acuerdo con su nivel jerárquico, realizando primero la de mayor jerarquía. Si existen paréntesis, deben resolverse primero los más internos y trabajar hacia fuera. En ausencia de paréntesis, la jerarquía de las operaciones es, de mayor a menor, la siguiente:

1.- Operación NOT

2.- Operación AND

3.- Operación OR

Si se tienen varias operaciones con la misma jerarquía, éstas pueden ser evaluadas de derecha a izquierda o de izquierda a derecha, el resultado será el mismo Como ejemplo, considérese la evaluación de las siguientes expresiones booleanas para A=1, B=0 y C=0.

Expresión :

$A B + B C' + A B' \,$

$1 0 + 0 0' + 1 0' \,$ (Sustitución de valores)

$1 0 + 0 1 + 1 1 \,$ (Evaluación de los NOT)

$0 + 0 + 1 \,$(Evaluación de los AND)

$0 + 1 \,$

$1 \,$(evaluación de los OR)

Circuitos combinacionales

Su definición es un conjunto de puerta conectadas entre si, cuya salida depende solo de la entrada en ese momento. La entrada viene seguida casi inmediatamente por la aparición de las salida. Por norma básica, se establece que un circuito combinacional, tiene n entradas binarias y m salidas binarias. Se definen tres formas:

1) Tabla de verdad: para cada 2^n combinaciones que se pueden realizar de las n entradas, se establece un valor para cada una de las m de salida.
2) Símbolo grafico, explica la forma en la que se organizan las interconexiones de las puertas del circuito.
3) Ecuaciones booleanas: cada señal se expresa en forma booleana de las señales de entrada.

Para poder realizar una simplificacion de estas expresiones, recurrimos a:

1)Simplificación algebraica, supone la reduccion de la expresion booleana en otra con menos elementos.
2) Mapas de Karnaugh, la funcion principal es simplificar mediante una función booleana, de cuatro a seis variables. Se estructura en un conjunto de 2^n cuadriculas.

Véase también

• Función booleana
• Formas Canónicas (Álgebra de Boole)
• Circuitos de conmutación
• Lógica binaria
• Puerta lógica
• Sistema digital
• Tabla de verdad

Enlaces externos

• Wikimedia Commons alberga contenido multimedia sobre Álgebra de Boole. Commons
• Álgebra de Boole y puertas lógicas
• Álgebra de Boole
• Álgebra de Boole
• Álgebra de Boole
• BOOLE-DEUSTO SW didáctico: Tablas de verdad, V-K, autómatas...
• Álgebra de Boole y Diseño de Computadoras (PDF)

Bibliografía

1. González Carlomán, Antonio. Universidad de Oviedo. Servicio de Publicaciones. ed. Retículo completo de Boole, lógica matemática, teoría de conjuntos (2006 edición). ISBN 84-8317-534-7. 
2. García Zubia, Javier; Sanz Martínez, Jesús; Sotomayor Basilio, Borja. Universidad de Deusto. Departamento de Publicaciones. ed. Boole-Deusto v2.1 entorno de diseño lógico (2005 edición). ISBN 84-7485-973-5. 
3. Giménez Pradales, José Miguel. Universidad Politécnica de Cataluña. Departamento de Matemática Aplicada III. ed. Álgebra de Boole para ingeniera técnica (2004 edición). ISBN 84-933451-0-5. 
4. García Zubia, Javier; Sanz Martínez, Jesús; Sotomayor Basilio, Borja. Universidad de Deusto. Departamento de Publicaciones. ed. Boole-Deusto entorno de diseño lógico (2004 edición). ISBN 84-7485-929-8. 
5. Ginés Gómez, José Carlos. Gines Gómez, José Carlos. ed. Puertas lógicas y álgebra de Boole, electrónica digital técnica de telecomunicación (1998 edición). ISBN 84-607-9518-7. 
6. Montes Lozano, Antoni. Editorial UOC, S.L.. ed. Álgebras de Boole (2002 edición). ISBN 84-8429-979-1. 
7. Montes Lozano, Antoni. Editorial UOC, S.L.. ed. Álgebras de Boole (2002 edición). ISBN 84-8429-926-0. 
8. González Carlomán, Antonio. Universidad de Oviedo. Servicio de Publicaciones. ed. Retículo completo de Boole. Lógica matemática teoría de conjuntos (2001 edición). ISBN 84-8317-264-X. 
9. Tiñena Salvañà, Francesc. Editorial UOC, S.L.. ed. Àlgebres de Boole (gestió) (1998 edición). ISBN 84-8318-582-2. 
10. Tiñena Salvañà, Francesc. Editorial UOC, S.L.. ed. Àlgebres de Boole (1998 edición). ISBN 84-8318-614-4. 
11. Permingeat, Noel; Glaude, Denis. Editorial Vicens-Vives, S.A.. ed. Álgebra de Boole (1993 edición). ISBN 84-316-3294-1. 
12. Masip Bruin, Xavier; Román Jiménez, José Antonio; Sánchez López, Sergio. Ediciones UPC, S.L.. ed. Álgebra de Boole y funciones lógicas (1996 edición). ISBN 84-89636-20-6. 
13. Jane Ihnsa, Ignacio. Universidad de Barcelona. Publicaciones y Ediciones. ed. Álgebras de Boole y lógica (1989 edición). ISBN 84-7875-040-1. 
14. Casanova, Gaston. Editorial Tecnos. ed. El álgebra de Boole (1975 edición). ISBN 84-309-0580-4. 
15. Martínez Garza, Jaime; Olvera Rodriguez. Organización y arquitectura de computadoras (2000 edición). ISBN 968-444-417-6.