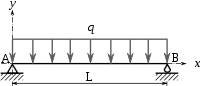
Pendientes y deformaciones en vigas
- Pendientes y deformaciones en vigas
-
Wikimedia foundation.
2010.
Mira otros diccionarios:
Viga — Para el grupo español de música, véase Viga (banda). Flexión teórica de una viga apoyada articulada sometida a una carga puntual centrada F. En ingeniería y arquitectura se denomina viga a un elemento constructivo lineal que trabaja… … Wikipedia Español
Curva elástica — Saltar a navegación, búsqueda La curva elástica o elástica es la deformada por flexión del eje longitudinal de una viga recta, la cual se debe a la aplicación de cargas transversales en el plano xy sobre la viga. Contenido 1 Ecuación de la… … Wikipedia Español
Flexión mecánica — Saltar a navegación, búsqueda En ingeniería se denomina flexión al tipo de deformación que presenta un elemento estructural alargado en una dirección perpendicular a su eje longitudinal. El término alargado se aplica cuando una dimensión es… … Wikipedia Español
Deflexión de sistemas estructurales — Saltar a navegación, búsqueda En análisis estructural, se considera a las deflexiones, como la respuesta estructural, por que expresa, un momento de parámetros, que responde, a una acción de cargas aplicadas (muertas, sismos, etc.), las… … Wikipedia Español
Pendiente de la recta — Saltar a navegación, búsqueda Para otros usos de este término, véase Pendiente. Pendiente de una carretera. En matemáticas y ciencias aplicadas se denomina pendiente a la inclinación de u … Wikipedia Español
Deflexión — Saltar a navegación, búsqueda En general, el término deflexión hace referencia a la desviación de la dirección de una corriente .[1] De un modo específico, el término deflexión se utiliza en física, análisis estructural, automovilística y… … Wikipedia Español