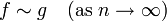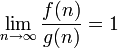Análisis asintótico

Análisis asintótico

Saltar a navegación, búsqueda

En matemáticas puras y aplicadas, en particular el análisis de algoritmos, el análisis asintótico es un método de descripción de la limitación de comportamiento. Limitar el comportamiento se expresa en el lenguaje de las relaciones de equivalencia. Además, el análisis asintótico se refiere a la solución de problemas aproximadamente hasta tales equivalencias. Por ejemplo, dado funciones de valor complejos f y g de una variable de número natural n, una forma escrita seria

$f \sim g \quad (\mbox{as } n\to\infty)$

y otra más común seria

$\lim_{n\to\infty} \frac{f(n)}{g(n)} = 1$

y f y g son llamados equivalente asintóticamente cuando n → ∞. Esto define una relación de equivalencia (en el conjunto de funciones distinto de cero para todos los n suficientemente grandes - la mayoría de los matemáticos prefieren la definición 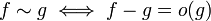$f\sim g\iff f-g=o(g)$ en cuanto a la notación de Landau, que evita esta limitación). La clase de equivalencia de f consta de todas las funciones g que "se comportan como" f, en el límite.

Obtenido de "An%C3%A1lisis asint%C3%B3tico"