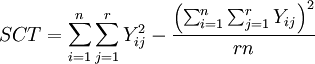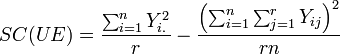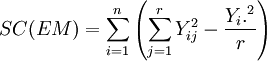Análisis de diseños experimentales con igual número de submuestras

Análisis de diseños experimentales con igual número de submuestras

Saltar a navegación, búsqueda

Se presenta un algoritmo general que, en sólo tres pasos, permite analizar los datos de cualquier diseño experimental con submuestreo en el que se haya tomado el mismo número de submuestras por unidad experimental.

Diseño experimental y análisis de varianza

Un diseño experimental sirve, generalmente, para comparar las medias de dos o más tratamientos (niveles de factor) a través del análisis de varianza, propuesto por Ronald A. Fisher a principios del Siglo XX, de los datos experimentales. Como es conocido, un experimento consiste en una manipulación intencional y controlada de una o más variables para evaluar su (supuesto) efecto en la variable dependiente o variable-respuesta. Dependiendo de las características del material experimental, el experimento puede hacerse en un diseño completamente aleatorizado (cuando el material experimental se supone sensiblemente homogéneo), en un diseño de bloques completos al azar (cuando se supone variación en una dirección), en diseño en cuadrados latinos (se asume que hay variación en dos direcciones); hay otras variantes de diseño experimental como el diseño grecolatino, parcelas divididas o anidado, bloques incompletos, bloques generalizados, entre otros. En otros términos, el diseño experimental involucra el arreglo físico de los diferentes niveles de factor cuando se realiza el experimento, según la variabilidad del material experimental; la partición de la variabilidad contenida en los datos experimentales en la variabilidad atribuida a las diferentes fuentes (de variación) se realiza a través del análisis de varianza. Este análisis permite obtener conclusiones sobre si hay diferencias o no entre las medias de los diferentes niveles de factor. La implicación de esta búsqueda es, entre otros ejemplos, encontrar la combinación de factores óptima que nos produce el material más resistente, hallar la mejor combinación de elementos que produce el mayor aumento de biomasa en seres vivos.

Aleatorización y toma de datos

Cada uno de los diseños experimentales, que se seleccionan de acuerdo a las características del material experimental y de los objetivos que persigue el experimentador, entraña un modo especial de realizar la aleatorización de los tratamientos sobre las unidades experimentales (o parcelas); de hecho, la aleatorización funciona como una especie de “seguro", según escriben Cochran y Cox en su libro de diseños experimentales de la década de los sesenta, que es una “prevención contra accidentes” que pueden ocurrir o no, y que en caso de ocurrir, pueden traer consecuencias graves o leves. Buscamos protegernos, obviamente, ante problemas graves. La aleatorización es una de las esencias en la realización de un experimento.

Otro punto que es crucial en relación al análisis de un experimento, es la toma de datos. Esto es, las mediciones que se hacen sobre la variable-respuesta. No importa qué tan bien se realice el experimento o qué diseño experimental tan minucioso o sofisticado se utilice, si la toma de datos no se hace en forma cuidadosa y correcta, no se puede esperar buenos resultados y las predicciones que se obtengan a partir del análisis de esos datos, no serán confiables. Así que, además de seleccionar el diseño adecuado y de planear y realizar cuidadosamente el experimento, se recomienda máximo cuidado en tomar los datos, para que éstos reflejen el comportamiento del fenómeno bajo estudio.

Diseños estándar y diseños con submuestreo

Se escribirá que un diseño experimental es estándar si en cada unidad experimental se toma sólo una observación al azar; si se toma más de una observación por unidad experimental se tendrá un diseño con submuestreo. Realizar el análisis de los diseños completamente al azar y bloques completos aleatorizados con submuestreo es relativamente fácil, puesto que los pasos y las fórmulas para dicho análisis se encuentran en los libros de diseños conocidos como el de Steel y Torrie (1985) o el de Martínez Garza (1988). En cambio, el análisis de un diseño experimental con submuestreo que no sea el de los dos diseños mencionados resulta, cuando menos, ambiguo, puesto que no aparece explícitamente la metodología en la literatura conocida. En estas notas se escribe el algoritmo de tres pasos para realizar dicho análisis. Esto es, se hace la extensión del análisis con submuestreo de los diseños básicos, el completamente aleatorizado (o de un factor) y el de bloques, que aparece en la literatura, a cualquier otro diseño experimental.

En la siguiente sección se comenta brevemente, sin abordar los detalles algebraicos, el razonamiento del algoritmo y de la forma como se desarrolló y comprobó. Los detalles pueden leerse en Zamudio y Alvarado (1996). De hecho como se verá, en la primera etapa del análisis, lo único que importa es el valor de la submuestra y la unidad experimental en la cual se registró. En la segunda etapa, para particionar la suma de cuadrados de las unidades en las sumas de cuadrados que corresponde al diseño experimental utilizado, lo que se hace es usar la suma de las observaciones de cada unidad dividida entre la raíz cuadrada del número de datos; el análisis se hace sobre este nuevo dato por unidad experimental usando las fórmulas o el algoritmo computacional para el diseño experimental correspondiente. El punto de cuidado es que la suma de cuadrados "total" obtenida en este segundo paso es, de hecho, la suma de cuadrados de las unidades experimentales, la que aparece como parte de la suma de cuadrados total en la Ecuación 1.

Variabilidad total de los datos experimentales

La variabilidad total, SC(total), de los datos de cualquier diseño experimental puede ser expresada como:

SCT = SC(UE) + SC(EM) (Ecuación 1)

La suma de cuadrados de las unidades experimentales, SC(UE), representa la variablidad de los datos que se presenta entre unidades experimentales. La suma de cuadrados del error de muestreo, SC(EM), refleja la variabilidad que hay en las unidades experimentales, es decir, la variabilidad entre observaciones tomadas en la misma unidad experimental. Aquí hay un detalle importante de aclarar: la ecuación es válida tanto si el diseño experimental es con submuestras o es estándar, excepto que en este último caso, la SC(EM) adquiere el valor de cero puesto que no es posible medir la variabilidad en la unidad experimental en tanto que sólo ha sido tomada una observación al azar.

A la ecuación 1 le llamaremos identidad general de las sumas de cuadrados y al modelo lineal que representa esta idea general lo nombraremos diseño de las unidades experimentales, que se escribe como sigue:

Yij = u + U_i + Eij (Ecuación 2)

donde Yij representa j-ésima observación tomada al azar de la i-ésima unidad experimental, u denota la media general, Ui representa a la i-ésima unidad experimental y Eij el ij-ésimo error aleatorio que representa la variabilidad de observaciones dentro de unidades, esto es, Eij es el error de muestreo. Se consideran n unidades experimentales -o parcelas - y r submuestras en cada una. En total, hay r n observaciones.

Algoritmo para analizar diseños experimentales con submuestreo

Acá sólo se aborda el caso en el que hay el mismo número de submuestras por unidad experimental; los casos con diferente número de submuestras no se incluye. El algoritmo es válido para cualquier diseño experimental específico con el mismo número de submuestras.

Suponer que en un experimento balanceado con n unidades experimentales se toman r submuestras por unidad experimental. El modelo lineal de este diseño, al que llamaremos diseño de las unidades experimentales está representado por la ecuación 2. Es importante remarcar que el diseño de las unidades experimentales es sólo una forma de conceptualizar cualquier diseño experimental. No es una forma de disponer físicamente las unidades experimentales en la práctica sino una estrategia que nos permite hacer comparables, en cuanto a su análisis, diseños experimentales diferentes. Enseguida los tres pasos:

PASO 1. Se ajusta un modelo basado en las unidades experimentales, calculando la suma de cuadrados total, SCT; la suma de cuadrados de las unidades experimentales, SC(UE); y la suma de cuadrados del error muestreo, SC(EM). En este paso se usan los datos originales, las Yij.

En este Paso 1, se emplean las siguientes fórmulas:

La suma de cuadrados total está dada por:

$SCT=\sum_{i=1}^n\sum_{j=1}^rY_{ij}^2-\frac{\left(\sum_{i=1}^n\sum_{j=1}^rY_{ij}\right)^2}{rn}$

La suma de cuadrados de la unidades experimentales, que define la variabilidad entre unidades experimentales, está dada por:

$SC(UE)=\frac{\sum_{i=1}^nY_{i.}^2}{r}-\frac{\left(\sum_{i=1}^n\sum_{j=1}^rY_{ij}\right)^2}{rn}$

La suma de cuadrados del error muestral, que define la variabilidad de observaciones dentro unidades experimentales, está dada por:

$SC(EM)=\sum_{i=1}^n\left(\sum_{j=1}^rY_{ij}^2-\frac{Y_i.^2}{r}\right)$

En estas fórmulas, Y_i. representa el total de la i-ésima unidad experimental y Y_.. es el gran total obtenido de sumar todas las observaciones de todas las unidades experimentales.

PASO 2. Ahora se ajusta un modelo usando una nueva variable-respuesta que denotaremos como Y_Nueva. La Y_Nueva se calcula así: (el total obtenido de sumar las submuestras de una unidad experimental) se divide entre (la raíz cuadrada del número de esas submuestras). Esta operación se hace en cada una de las unidades experimentales. Esto es, la Y_Nueva está dada por: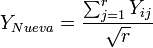

$Y_{Nueva}=\frac{\sum_{j=1}^rY_{ij}}{\sqrt{r}}$

Nota: Observe que las rn observaciones Y_ij originales se convierten ahora en sólo n Y_Nueva, una que corresponde a cada unidad experimental.

¿Qué se hace con la nueva variable respuesta, Y_Nueva?

Con Y_Nueva se ajusta el modelo que corresponde al diseño experimental en que obtuvo los datos. Esto es, si los datos provienen de un diseño completamente aleatorizado, se calculan las sumas de cuadrados de tratamientos, del error y del "total", con la Y_Nueva. Si los datos provienen de un diseño de bloques completos al azar, se requiere calculas las Sumas de cuadrados de bloques (SCbloq), Suma de cuadrados de tratamiento y Suma de cuadrados del Error; si los datos provienen de un diseño de cuadrado latino, se calculan las sumas de cuadrados de hileras, columnas, error y "total", y así en seguida. Estos cálculos deben hacerse considerando a Y_Nueva como si observación "registrada" en las unidades experimentales.

Esta operación permite particionar las SC(UE) obtenida en el Paso 1, en las sumas de cuadrados de las fuentes correspondientes al diseño experimental particular de donde se tomaron los datos.

Es conveniente observar que las sumas de cuadrados "total" obtenidas con la Y_Nueva en este Paso 2, corresponderán a la SC(UE) obtenida en el Paso 1.

PASO 3. Se combinan las sumas de cuadrados de los pasos 1 y 2 en una una nueva tabla y se tiene el Análisis de Varianza (ANOVA) del diseño experimental con submuestreo.

Enlaces externos

• Principios básicos del diseño de experimentos
• http://agronomia.unal.edu.co/documentos/ejercici.pdf

Fuentes

• Cochran y Cox. (1974). Diseños experimentales. México: Trillas.
• Martínez-Garza, A. (1988). Diseños experimentales: métodos y elementos de teoría. México: Trillas.
• Searle, S. R. (1990). Matrix Algebra useful for statistics.USA: John Wiley and Sons.
• Snedecor, G. y W. Cochran. (1967). Statistical methods. Sixth edition. Ames, USA: Iowa State University.
• Steel, R. y J. Torrie. (1988). Bioestadística: principios y procedimientos. 2da edición. México: McGrawHill.
• Zamudio S., Francisco J.; Arturo A. Alvarado S. (1996). Análisis de diseños experimentales con igual número de submuestras. México: Universidad Autónoma Chapingo. 83 p.

Obtenido de "An%C3%A1lisis de dise%C3%B1os experimentales con igual n%C3%BAmero de submuestras"