- Análisis funcional
-
Análisis funcional
El análisis funcional es la rama de las matemáticas, y específicamente del análisis, que trata del estudio de espacios de funciones. Tienen sus raíces históricas en el estudio de transformaciones tales como transformación de Fourier y en el estudio de las ecuaciones diferenciales y ecuaciones integrales. La palabra funcional se remonta al cálculo de variaciones, implicando una función cuyo argumento es una función. Su uso en general se ha atribuido a Volterra.
En la visión moderna inicial, se consideró el análisis funcional como el estudio de los espacios vectoriales normados completos sobre los reales o los complejos. Tales espacios se llaman Espacios de Banach. Un ejemplo importante es el espacio de Hilbert, donde la norma surge de un producto escalar. Estos espacios son de importancia fundamental en la formulación matemática de la mecánica cuántica. Más general y modernamente, el análisis funcional incluye el estudio de los espacios de Fréchet y otros espacios vectoriales localmente convexos y aún topológicos.
Un objeto importante de estudio en análisis funcional son los operadores lineales continuos definidos en los espacios de Banach y de Hilbert. Éstos conducen naturalmente a la definición de C* álgebra y otras álgebras de operadores.
Los espacios de Hilbert pueden ser clasificados totalmente: hay un espacio único de Hilbert módulo isomorfismo para cada cardinal de la base (hilbertiana). Puesto que los espacios de Hilbert finito-dimensionales se entienden completamente en álgebra lineal, y puesto que los morfismos de los espacios de Hilbert se pueden dividir siempre en morfismos de espacios con dimensionalidad alef-0 (
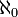 ), análisis funcional de Hilbert trata sobre todo con el espacio único de Hilbert de dimensionalidad alef-0, y sus morfismos.
), análisis funcional de Hilbert trata sobre todo con el espacio único de Hilbert de dimensionalidad alef-0, y sus morfismos.Los espacios de Banach generales son mucho más complicados que los espacios de Hilbert. No hay definición clara de qué constituiría una base, por ejemplo.
Para cualquier número real p ≥ 1, un ejemplo de un espacio de Banach viene dado por los espacios Lp).
En los espacios de Banach, una gran parte del estudio involucra al espacio dual: el espacio de todas funcionales lineales continuas. Como en álgebra lineal, el dual del dual no es siempre isomorfo al espacio original, pero hay un monomorfismo natural de un espacio en su doble dual siempre. Esto se explica en el artículo espacio dual.
La noción de derivada se amplía a las funciones arbitrarias entre los espacios de Banach; resulta que la derivada de una función en cierto punto es realmente una función lineal continua.
Aquí enumeramos algunos resultados importantes del análisis funcional:
- Teorema de Banach-Steinhaus es un resultado en conjuntos equicontinuos de operadores.
- Teorema espectral da una fórmula integral para los operadores normales en un espacio de Hilbert. Es de importancia central en la formulación matemática de la mecánica cuántica.
- Teorema de Hahn-Banach es sobre la extensión de funcionales continuos desde un subespacio a todo el espacio, de una manera que preserve la norma.
- Teorema de la función abierta y teorema de la gráfica cerrada.
- Teorema del punto fijo de Banach
Referencias
- Yosida, K.: Functional Analysis, Springer-Verlag, 6th edition, 1980
- Schechter, M.: Principles of Functional Analysis, AMS, 2nd edition, 2001
- Hutson, V., Pym, J.S., Cloud M.J.: Applications of Functional Analysis and Operator Theory, 2nd edition, Elsevier Science, 2005, ISBN 0-444-51790-1
- Dunford, N. and Schwartz, J.T. : Linear Operators, General Theory, and other 3 volumes, includes visualization charts
- Brezis, H.: Analyse Fonctionnelle, Dunod
- Sobolev, S.L.: Applications of Functional Analysis in Mathematical Physics, AMS, 1963
- Lebedev, L.P. and Vorovich, I.I.: Functional Anlysis in Mechanics, Springer-Verlag, 2002
Categoría: Análisis funcional
Wikimedia foundation. 2010.
