- Paridad de una función
-
Paridad de una función
En matemáticas, se puede clasificar a las funciones según su paridad. Las funciones pueden ser pares, impares o no tener paridad. Aquellas funciones que poseen paridad satisfacen una serie de relaciones particulares de simetría, con respecto a inversas aditivas. Las funciones pares e impares son importantes en muchas áreas del análisis matemático, especialmente en la teoría de las series de potencias y series de Fourier. Deben su nombre a la paridad de las potencias de las funciones de potencia que satisfacen cada condición:
la función xn
- es una función par si n es un entero par,
- y es una función impar si n es un entero impar.
Contenido
Funciones pares
Sea f(x) una función de valor real de una variable real. Entonces f es par si se satisface la siguiente ecuación para todo x en el dominio de f:
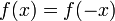 .
.
Desde un punto de vista geométrico, una función par es simétrica con respecto al eje y, lo que quiere decir que su gráfica no se altera luego de una reflexión sobre el eje y.
Ejemplos de funciones pares son el valor absoluto, x2, x4, cos(x), y cosh(x).
Funciones impares
Nuevamente, sea f(x) una función valor real de una variable real. Entonces f es impar si se satisface la siguiente ecuación para todo x en el dominio de f:
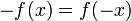 .
.
Desde un punto de vista geométrico, una función impar posee una simetría rotacional con respecto al origen de coordenadas, lo que quiere decir que su gráfica no se altera luego de una rotación de 180 grados alrededor del origen.
Ejemplos de funciones impares son x, x3, seno(x), sinh(x), y la erf (x).
Características
Nota: Que una función sea par o impar no implica que sea diferenciable, o su continuidad.
Propiedades
- La única función que es tanto par e impar es la función constante que es idénticamente cero (o sea f(x) = 0 para todo x).
- La suma de una función par y una impar no es ni par ni impar, a menos de que una de las funciones sea el cero.
- La suma de dos funciones par es una función par, y todo múltiplo de una función par es una función par.
- La suma de dos funciones impares es una función impar, y todo múltiplo constante de una función impar es una función impar.
- El producto de dos funciones pares es una función par.
- El producto de dos funciones impares es una función par.
- El producto de una función par y una función impar es una función impar.
- El cociente de dos funciones pares es una función par.
- El cociente de dos funciones impares es una función par.
- El cociente de una función par y una función impar es una función impar.
- La derivada de una función par es una función impar.
- La derivada de una función impar es una función par.
- La composición de dos funciones pares es una función par, y la composición de dos funciones impares es una función impar.
- La composición de una función par y una función impar es una función par.
- la composición de toda función con una función par es par (pero no vice versa).
- La integral de una función impar entre -A y +A es cero (donde A es finito, y la función no posee ninguna asíntota vertical entre -A y A).
- La integral de una función par entre -A y +A es el doble de la integral entre 0 y +A (donde A es finito, y la función no posee ninguna asíntota vertical entre -A y A).
Series
- La serie de Maclaurin de una función par se compone solo de términos con potencias pares.
- La serie de Maclaurin de una función impar se compone solo de términos con potencias impares.
- La serie de Fourier de una función par periódica solo incluye términos cosenos.
- La serie de Fourier de una función impar periódica solo incluye términos senos.
Referencias
Véase también
- Función hermitiana para una generalización a los números complejos.
- Serie de Taylor
- Series de Fourier
- Función par
- Función impar
Categorías: Cálculo | Funciones
Wikimedia foundation. 2010.



