- Plasticidad (mecánica de sólidos)
-
Plasticidad (mecánica de sólidos)
La plasticidad es la propiedad mecánica de un material, biológico o de otro tipo, de deformarse permanentemente e irreversiblemente cuando se encuentra sometido a tensiones por encima de su rango elástico, es decir, por encima de su límite elástico.
En los metales, la plasticidad se explica en términos de desplazamientos irreversibles de dislocaciones.
Contenido
Introducción
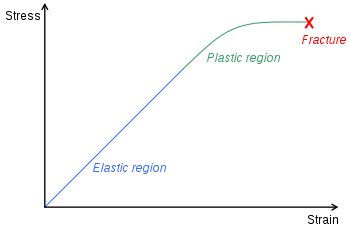
En los materiales elásticos, en particular en muchos metales dúctiles, un esfuerzo de tracción pequeño lleva aparejado un comportamiento elástico. Eso significa que pequeños incrementos en la tensión de tracción comporta pequeños incrementos en la deformación, si la carga se vuelve cero de nuevo el cuerpo recupera exactamente su forma original, es decir, se tiene una deformación completamente reversible. Sin embargo, se ha comprobado experimentalmente que existe un límite, llamado límite elástico, tal que si cierta función homogénea de las tensiones supera dicho límite entonces al desaparecer la carga quedan deformaciones remanentes y el cuerpo no vuelve exactamente a su forma. Es decir, aparecen deformaciones no-reversibles.
Este tipo de comportamiento elasto-plástico descrito más arriba es el que se encuentra en la mayoría de metales conocidos, y también en muchos otros materiales. El comportamiento perfectamente plástico es algo menos frecuente, e implica la aparición de deformaciones irreversibles por pequeña que sea la tensión, la arcilla de modelar y la plastilina se aproximan mucho a un comportamiento perfectamente plástico. Otros materiales además presentan plasticidad con endurecimiento y necesitan esfuerzos progresivamente más grandes para aumentar su deformación plástica total. E incluso los comportamientos anteriores puden ir acompañados de efectos viscosos, que hacen que las tensiones sean mayores en casos de velocidades de deformación altas, dicho comportamiento se conoce con el nombre de visco-plasticidad.
La plasticidad de los materiales está relacionada con cambios irreversibles en esos materiales. A diferencia del comportamiento elástico que es termodinámicamente reversible, un cuerpo que se deforma plásticamente experimenta cambios de entropía, como desplazamientos de las dislocaciones. En el comportamiento plástico parte de la energía mecánica se disipa internamente, en lugar de transformarse en energía potencial elástica.
Microscópicamente, en la escala de la red cristalina de los metales, la plasticidad es una consecuencia de la existencia de ciertas imperfecciones en la red llamadas dislocaciones. En 1934, Egon Orowan, Michael Polanyi y Geoffrey Ingram Taylor, más o menos simultaneamente llegaron a la conclusión de que la deformación plástica de materiales dúctiles podía ser explicada en términos de la teoría de dislocaciones. Para describir la plasticidad usualmente se usa un conjunto de ecuaciones diferenciales no lineales y no integrables que describen los cambios en las componentes del tensor deformación y el tensor tensión con respecto al estado de deformación-tensión previo y el incremento de deformación en cada instante.
Historia de la disciplina
La base de la moderna teoría de la plasticidad fue asentada en el siglo XIX con los trabajos de Tresca, Saint-Venant, Lévy y Bauschinger. A principios del siglo XX se hicieron algunos avances en la comprensión del fenómeno por parte de Prandtl, Von Mises y A. Reuss. En esta primera fase se introdujo el concepto de deformación irreversible, criterios de fallo, endurecimiento y plasticidad perfecta, además de la forma incremental de las ecuaciones constitutivas de la deformación plástica.
Justo después de la Segunda Guerra Mundial aparecieron los trabajos de Prager, Drucker y Hill se logró una mayor claridad de la formulación y se estableció la convexidad de las superficies de fluencia. Poco después, a partir de 1960, se produjeron ciertos avances matemáticos en la teoría de ecuaciones en derivadas parciales y las desigualdades variacionales que resultarían ser particularmente provechosos para la teoría de la plasticidad. Esos avances probaron que el marco natural para resolver los problemas de valor incial en sólidos elastoplásticos eran las desigualdades variacionales. La confluencia de ciertos avances en el terreno de la mecánica de sólidos y las matemáticas dieron lugar a nuevos desarrollos teóricos, de los cuales son un ejemplo los artículos de Moreau, las monografías de Duvaut y J.L. Lions y Temam.
Modelos de plasticidad
En general un modelo de plasticidad requiere definir varios elementos:
- En primer lugar en el espacio de tensiones principales se requiere definir la llamada región de tensiones admisibles, que será un conjunto cerrado (y posiblemente compacto) de dicho espacio de tensiones. La frontera de dicho conjunto usualmente se denomina superficie de fluencia.
- Para puntos del sólido cuyas tensiones principales estén contenidas en el interior de la región de tensiones admisibles el comportamiento es elástico. Sin embargo, para puntos de la superficie de fluencia es necesario definir una "regla de flujo" que explicita como aumentarán la deformación plástica en función de la tasa de aumento de la tensión y otros parámetros.
- Los modelos de plasticidad imperfecta requerirán la definición de un conjunto de variables internas que den cuenta del endurecimiento y del desplazamiento de la región de tensiones admisibles a lo largo del tiempo en función de las tasas de aumento de las otras variables.
Ecuaciones constitutivas de plasticidad
La ley de Hooke usada para materiales elásticos reversibles y lineales es una ecuación constitutiva en que las tensiones se describen como el producto de componentes tensoriales del tensor de constantes elásticas por las componentes del tensor deformación. En dicha ley las tensiones son combinaciones lineales de las deformaciones, y no existe potencia disipación de energía y por tanto irreversibilidad. Por esas razones no pueden describir la plasticidad. De hecho la descripción matemática de la plasticidad debe incluir tanto la irreversibilidad o disipación de energía como la no-linealidad de las expresiones que relacionan tensiones y deformaciones. De hecho, existen un buen número de modelos matemáticos de plasticidad con estas características. En todos los modelos de plasticidad la relación entre tensiones y deformaciones son del tipo:
(1)
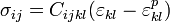
Donde en la ecuación anterior y en las siguientes se usa el convenio de sumación de Einstein sobre índices repetidos, y donde además:
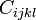 , son las componentes del tensor de constantes elásticas del material.
, son las componentes del tensor de constantes elásticas del material.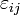 , son las componentes del tensor deformación.
, son las componentes del tensor deformación.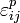 , son las componentes de la deformación plástica.
, son las componentes de la deformación plástica.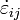 , representan la velocidad de deformación.
, representan la velocidad de deformación.
La diferencia básica entre los diversos modelos de plasticidad es la superficie de fluencia y por tanto la manera en que se computan las deformaciones plásticas, además de las posibles variaciones en la componente viscoplástica. De hecho un modelo de plasticidad además de la ecuación () necesita especificar dos relaciones más:
- Especificacación de la superficie de fluencia, que relaciona la tensión de fluencia
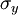 con el estado de tensión y de deformación plástica:
con el estado de tensión y de deformación plástica:
(2)
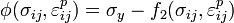
- La ley de flujo plástico:
(3)
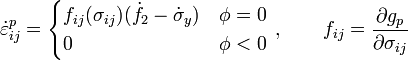
Modelo de plasticidad J2
Este es un modelo elasto-plástico isótropo sin vicosidad ni endurecimiento y es uno de los modelos elasto-plásticos más sencillos. La tensión en cada instante viene dada por una tensión puramente elástica independiente de la velocidad de deformación:
(1a)
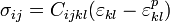
Donde la superficie de fluencia y la zona plástica vienen dadas por el segundo invariante o invariante cuadrático del tensor desviador.
(2a)
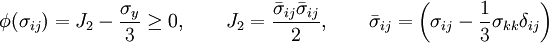
Las ecuaciones básicas adicionales de la evolución temporal del límite de fluencia y la deformación elástica son:
(2b)
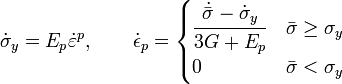
Donde:
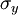 , es la tensión de fluencia.
, es la tensión de fluencia.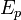 , es el módulo de elasticidad longitudinal en el dominio plástico.
, es el módulo de elasticidad longitudinal en el dominio plástico.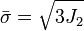
Siendo las condiciones iniciales existentes antes de la aparición de plastificación son:

Modelo elastoplástico hidrodidámico
Este modelo atribuye un comportamiento elástico al material por debajo de límite de fluencia y atribuye aumentos de la deformación plástica por encima de él. La velocidad de deformación no juega ningún papel dentro de él. Las relaciones entre tensión y deformación son de la forma:
(1b)
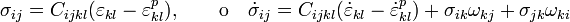
Donde la superficie de fluencia y la zona donde se producen deformaciones plástica es la misma que en el modelo de plasticidad J2, lo cual significará que existirá aumento de la deformación plástica siempre y cuando:
(2c)
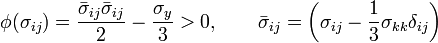
(2d)
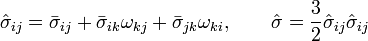
Las ecuaciones adicionales de la evolución temporal del límite de fluencia y la deformación plástica son:
(2e)
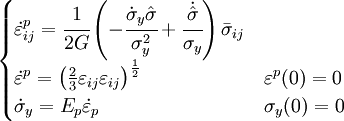
Donde el instante inicial se ha tomado antes de que apareciera plastificación.
Modelo visco-elastoplástico de Krieg-Key
Este modelo es un modelo elasto-plástico con endurecimiento cinemático, una vez pasado el punto de fluencia del material. La relación entre tensiones y deformaciones viene dada por una contribución elástica más una contribución plástica. En el caso isotrópico la superficie de fluencia se toma como el lugar geométrico:[1]
(2f)
![\phi = \frac{\sigma_y^2}{3} -\frac{\bar{\sigma}_{ij} - \alpha_{ij}}{2} = 0, \qquad
\sigma_y = \left[ 1+ \left( \frac{\dot{\varepsilon}_{ij}\dot{\varepsilon}_{ij}}{C^2} \right)^\frac{1}{2p} \right]
(\sigma_0 + \beta E_p \varepsilon_{eff}^p)](/pictures/eswiki/53/52ce7db19cb09a32921f90881394c8cd.png)
Donde:
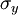 recibe el nombre de tensión de fluencia.
recibe el nombre de tensión de fluencia.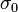 , es un parámetro que define la superficie de fluencia, cuando las tensiones caen fuera de la superficie de fluencia se acumula más deformación plástica.
, es un parámetro que define la superficie de fluencia, cuando las tensiones caen fuera de la superficie de fluencia se acumula más deformación plástica.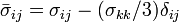 , son las componentes de la parte desviadora del tensor tensión.
, son las componentes de la parte desviadora del tensor tensión.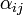 es la velocidad de deformación co-rotacional que puede obtenerse a partir de la derivada temporal del tensor deformación mediante:
es la velocidad de deformación co-rotacional que puede obtenerse a partir de la derivada temporal del tensor deformación mediante:
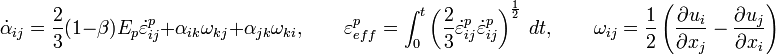
La versión isótropa de este modelo contiene 7 constantes del material: dos constantes elásticas
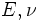 , dos parámetros de de plasticidad
, dos parámetros de de plasticidad 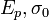 , dos parametros de viscoelásticos
, dos parametros de viscoelásticos 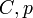 y el parámetro de endurecimiento
y el parámetro de endurecimiento 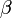 .
.Plasticidad en los metales
Cálculo plástico
El cálculo plástico se refiere al cálculo de esfuerzos, tensiones y deformaciones en ingeniería estructural de elementos que tienen un comportamiento plástico. A diferencia de los mecanismos que deben operar de manera reversible las estructuras estáticas pueden ser proyectadas para trabajar por encima del dominio elástico, lográndose con ello un aprovechamiento más completo de su capacidad resistente. Esto se debe a que una vez rebasado el dominio elástico de reversibilidad, algunos materiales de construcción siguen teniendo capacidad para resistir esfuerzos mayores, por endurecimiento cinemático, aún a costa de sufrir transformaciones internas irreversibles.
En estructura metálica el cálculo plástico consiste básicamente en identificar los puntos de aparición de rótulas plásticas o regiones de plastificación que una vez completamente plastificadas se convierten en articulaciones. La aparición de articulaciones reducen el grado de hiperestaticidad ampliando el número de grados de libertad. Cuando aparecen el suficiente número de rótulas plásticas la estructura se convierte en un mecanismo. El cálculo plástico incluye la identificación de los modos de colapso por formación de rótulas plásticas, y la carga necesaria para la plastificación de todas las rótulas.
También en el cálculo de estructuras de hormigón armado se admite que las barras de acero sometidas a tracción adquieran deformaciones plásticas, ya que el acero tiene un comportamiento plástico con endurecimiento, y al rebasar su límite elástico se endure pudiéndo soportar mayores tensiones que antes de adquirir deformaciones plásticas. Este endurecimiento o aumento de la capacidad resistente del acero en tracción permite economizar, y construir estructuras con una menor cantidad de acero.
Plasticidad de los suelos
En el caso de algunos terrenos húmedos, la plasticidad es la propiedad que les permite ser moldeados aplicándoles fuerzas externas, y mantener las formas adquiridas, aun cuando la humedad y las fuerzas externas desaparezcan. Según Atterberg[2] se pueden definir dos límites de plasticidad,[3] el máximo y el mínimo. Con porcentaje de humedad por encima del límite máximo de plasticidad, la masa terrosa adquiere fluidez y pierde su capacidad de mantener la forma, y si el terreno tiene un porcentaje de humedad por debajo del límite mínimo de plasticidad, la masa terrosa se vuelve quebradiza, y no se puede moldear.[4] Es evidente que no todos los suelos tienen la misma plasticidad; las arenas y los limos tienen una plasticidad baja o muy baja, mientras que suelos con alto contenido de arcillas tienen una plasticidad mayor. En línea general puede afirmarse que terrenos con un contenido de arcilla inferior al 15% no son plásticos[5]
Para cada uno de los límites de plasticidad, el máximo y el mínimo, corresponde, en función del terreno, un porcentaje de humedad, la diferencia entre los dos porcentajes de humedad límites de llama número o índice de plasticidad. Tanto los límites de plasticidad como también el correspondiente número de plasticidad o índice de plasticidad varían, obviamente de terreno a terreno, en función principalmente de la textura y más precisamente del contenido de coloides inorgánicos.
Otro factor importante que influencia la plasticidad es el tipo de cationes disponibles.[6] Generalmente el ión K+ disminuye los dos límites de plasticidad y el índice de plasticidad, mientras que el ión Na+ disminuye los límites de plasticidad, pero aumenta el índice de plasticidad; los cationes Mg++ y Ca++ aumentan la plasticidad, pero los terrenos saturados con ellos requieren una cantidad elevada de agua para alcanzar el estado de plasticidad, al contrario de los saturados con cationes de K+. El efecto de hidratación y de dispersión del Na+ determinan una plasticidad de los suelos saturados con este catión mayor de la que alcanzan los terrenos saturados con cationes bivalentes.
Generalmente, la influencia de los diversos cationes sobre la plasticidad varia con la calidad y la naturaleza de la arcilla.
La materia orgánica contenida en el suelo también tiene un efecto importante en la plasticidad de los suelos.[7] En general los estratos superiores del suelo tienen una plasticidad mayor que los estratos más profundos. Esto puede atribuirse a la mayor presencia de material orgánico en las capas superiores del terreno.
Referencias
- ↑ Krieg, R.D. and Key, S.W., Implementation of a time dependent plasticity theory into structural computer programs. In: Stricklin, J.A., Saczalski, K.J. (Eds.), Constitutive Equations in Viscoplasticity: Computational and Engineering Aspects, AMD-20, ASEM, New York. pp. 125-137.
- ↑ Ver también: Límites de Atterberg
- ↑ T.William Lambe, Mecánica de Suelos. Impreso en México,1997. ISBN 968-18-1894-6
- ↑ Constantino Constantinidis. Bonifica ed irrigazione. Edagricole, Bologna, 1970
- ↑ C. Constantinidis. 1970. pag.186-187.
- ↑ Baver, L.D. - 1928. The Relation of Exchangeable Cations to the Phisical Properties of Soils. J.Am.Soc.Agron., 20: 921-941.
- ↑ Baver, L.D. - 1930. The effect of Organic Matter Upon Several Physical Properties of Soils. J.Am.Soc.Agron., 22: 703-708.
Categorías: Mecánica de medios continuos | Ingeniería estructural | Ingeniería geotécnica | Materiales por propiedades físicas
Wikimedia foundation. 2010.