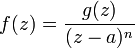- Polo (análisis complejo)
-
Polo (análisis complejo)
En análisis complejo, un polo de una función holomorfa es un cierto tipo de singularidad que se comporta como la singularidad 1/zn en z = 0. Un polo de la función f(z) es un punto z = a tal que f(z) tiende a infinito a medida que z tiende a a.
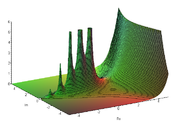 El valor absoluto de la Función gamma. La imagen muestra que la función tiende a infinito en los polos (izquierda). En la parte derecha, la función Gamma no tiene polos, únicamente se incrementa rápidamente.
El valor absoluto de la Función gamma. La imagen muestra que la función tiende a infinito en los polos (izquierda). En la parte derecha, la función Gamma no tiene polos, únicamente se incrementa rápidamente.
Formalmente, sea U un subconjunto abierto del plano complejo C, sea a un elemento de U y f : U − {a} → C es una función holomorfa . Si existe una función holomorfa g : U → C y un número natural n tal que tal que
para toda z de U − {a}, entonces llamamos a a polo de f. Si el entero n, se escoge tan pequeño como sea posible, entonces n se le denomina orden del polo. Un polo de orden 1 también es llamado polo simple.
Equivalentemente, a es un polo de orden n≥ 0 de una función f si existe un entorno abierto U de a tal que f : U - {a} → C es holomorfa y el límite :
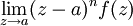 existe y es diferente de 0.
existe y es diferente de 0.El punto a es un polo de orden n de f si y solo si todos lo términos de la serie de Laurent de f definidos en el entorno de a de grado inferior a n se anulan y el término de grado n es distinto de cero.
Un polo de orden 0 es una singularidad removible. En este caso, el límite limz→a f(z) existe como número complejo, y la funcion puede ser representada por una serie de Taylor. Si el orden es mayor que 0, entonces limz→a f(z) = ∞, y la funcion tendra un desarrollo en terminos de la serie de Laurent.
Si la primera derivada de la función f tiene un polo simple en a, entonces a es un punto de ramificación de f. (El recíproco no tiene porque ser cierto).
Una singularidad no removible que no es un polo ni un punto de ramificación se le llama singularidad esencial.
Una función holomorfa cuyas todas sus singularidades son polos se le denomina función meromorfa.
Véase también
Categoría: Análisis complejo
Wikimedia foundation. 2010.