- Potencia de un conjunto
-
Potencia de un conjunto
La potencia de un conjunto es un conjunto definido a partir de las propiedades del producto cartesiano. No debe confundirse este concepto con el de conjunto potencia que se obtiene sin recurrir a las propiedades del producto cartesiano.
Contenido
Potencia de un conjunto ordinario
Dado un conjunto ordinario
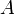 que no representa ninguna estructura particular se define la n-ésima potencia como la aplicación iterada del producto cartesiano:
que no representa ninguna estructura particular se define la n-ésima potencia como la aplicación iterada del producto cartesiano: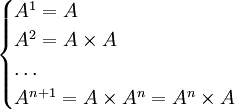
La definición anterior puede extenderse a potencias infinitas donde n puede ser un número ordinal cualquiera, no necesariamente finito.
Potencia de una relación binaria
Dada una relación binaria
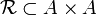 definida sobre un conjunto A se definen las potencias de dicha relación mediante:
definida sobre un conjunto A se definen las potencias de dicha relación mediante: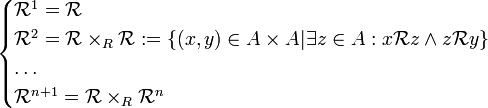
La noción de potencia de relación permite por ejemplo construir la clausura transitiva de una relación binaria cualquiera como unión generalizada de las sucesivas potencias.
Potencia tensorial
Dado un espacio vectorial
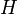 se pueden definir sus potencias tensoriales
se pueden definir sus potencias tensoriales 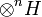 mediante el producto tensorial ordinario:
mediante el producto tensorial ordinario: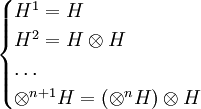
Potencia de un número ordinal
Véase también: Número ordinalCategoría: Teoría de conjuntos
Wikimedia foundation. 2010.
