Principio de d'Alembert

Principio de d'Alembert

Saltar a navegación, búsqueda

Retrato de Jean d'Alembert.

El principio de d'Alembert, enunciado por Jean d'Alembert en su obra maestra Tratado de dinámica de 1743, establece que la suma de las fuerzas externas que actúan sobre un cuerpo y las denominadas fuerzas de inercia forman un sistema de fuerzas en equilibrio. A este equilibrio se le denomina equilibrio dinámico.

Enunciado e Historia

El principio de d'Alembert establece que para todas las fuerzas de un sistema:

$\sum_i (\dot{\mathbf{p}}_i - \mathbf{F}_i)\cdot \delta\mathbf{r}_i = 0$

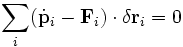
Donde la suma se extiende sobre todas las partículas del sistema, siendo:

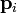$\mathbf{p}_i$, momento de la partícula i-ésima.

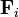$\mathbf{F}_i$, fuerza sobre la partícula i-ésima.

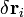$\delta \mathbf{r}_i$ cualquier campo vectorial de desplazamientos virtuales sobre el conjunto de partículas que sea compatible con los enlaces y restricciones de movimiento existentes.

El principio de d'Alembert es realmente una generalización de la segunda ley de Newton en una forma aplicable a sistemas con ligaduras. Por otra parte el principio equivale a las ecuaciones de Euler-Lagrange. Lagrange usó este principio bajo el nombre de principio de velocidades generalizadas, para encontrar sus ecuaciones, en la memoria sobre las libraciones de la Luna de 1764, abandonando desde entonces el principio de acción y basando todo su trabajo en el principio de D'Alembert durante el resto de su vida y de manera especial en su Mécanique Analytique. Tal cambio de actitud pudo estar influido por dos razones:^[1]

• En primer lugar, el principio de acción estacionaria está ligado a la existencia de una función potencial, cuya existencia no requiere en el principio de d'Alembert.
• En segundo lugar, el principio de acción se presta a interpretaciones filosóficas y teleológicas que no le gustaban a Lagrange.

Finalmente debe señalarse que el principio de d'Alembert es peculiarmente útil en la mecánica de sólidos donde puede usarse para plantear las ecuaciones de movimiento y cálculo de reacciones usando un campo de desplazamientos virtuales que sea diferenciable. En ese caso el cálculo mediante el principio de D'Alembert, que también se llama en ese contexto principio de los trabajos virtuales es ventajoso sobre el enfoque más simple de la mecánica newtoniana.

Derivación

Consecuencias

El principio de d'Alembert en el caso de existir ligaduras no triviales lleva a las ecuaciones de Euler-Lagrange, si se usa conjunto de coordenadas generalizadas independientes que implícitamente incorporen dichas ligaduras. Consideremos un sistema de N partículas en el que existan m ligaduras:

$G_k(\mathbf{r}_1,\cdots,\mathbf{r}_N) = 0$

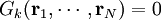
Por el teorema de la Función Implícita existirán n = 3N-m coordenadas generalizadas y N funciones vectoriales tales que:

$\mathbf{r}_i = \mathbf{h}_i(q_1,...,q_n)$

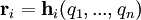
El principio de d'Alembert en las nuevas coordenadas se expresará simplemente como:

(4) $\sum_{i=1}^N (\mathbf{F}_i - \dot\mathbf{p}_i)\cdot\delta\mathbf{r}_i = \sum_{j=1}^n (Q_j - W_j)\delta q_j \qquad \Rightarrow \qquad (Q_j - W_j) = 0$

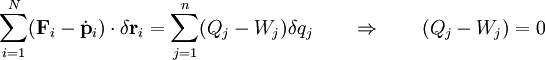
La última implacación se sigue de que ahora todas las 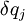$\delta q_j\;$ son independientes. Además la fuerza generalizada Q_j y el término W_j vienen dados por:

$Q_j = \sum_i \frac{\part \mathbf{r}_i}{\part q_j}, \qquad W_j = \sum_i \dot\mathbf{p}_i \frac{\part \mathbf{r}_i}{\part q_j} = \sum_i \dot\mathbf{p}_i \frac{\part \dot\mathbf{r}_i}{\part \dot{q}_j} =\left[ \sum_i \frac{d}{dt} \left(\mathbf{p}_i \frac{\part \dot\mathbf{r}_i}{\part \dot{q}_j}\right) - \sum_i \mathbf{p}_i \frac{d}{dt}\left(\frac{\part \mathbf{r}_i}{\part q_j}\right)\right]$

Expresando W_j en términos de la energía cinética T tenemos:

$W_j = \sum_i \frac{d}{dt} \left(\frac{\part T}{\part \dot\mathbf{r}_i} \frac{\part \dot\mathbf{r}_i}{\part \dot{q}_j}\right) - \sum_i \frac{\part T}{\part \dot\mathbf{r}_i} \frac{\part \dot\mathbf{r}_i}{\part q_j} = \quad \frac{d}{dt}\left(\frac{\part T}{\part \dot{q}_j}\right)-\frac{\part T}{\part q_j}$

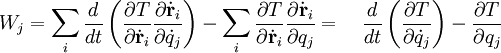
Y por tanto finalmente usando (4) llegamos a las ecuaciones de Euler-Lagrange:

(5) $\frac{d}{dt}\left(\frac{\part T}{\part \dot{q}_j}\right)-\frac{\part T}{\part q_j} = Q_j$

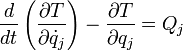
Si las fuerzas son además conservativas entonces podemos existe una función potencial U(W_j) y podemos definir el lagrangiano L = T - U, simplificando aún más la expresión anterior.

Referencias

1. ↑ Fernández Rañada, 2005, p. 133.

• L. Meirovichm: Methods of analytical dynamics, McGraw-Hill, New York, 1970.
• H. Goldstein: Mecánica clásica, 2ª edición, Reverté, Barcelona, 1987.
• Fernádez Rañada, Antonio (2005). «4», Fondo de Cultura Económica (ed.). Dinámica Clásica, 1ª edición, pp. 131-133. ISBN 84-206-8133-4.

Véase también

• Dinámica
• Principio de los trabajos virtuales

Obtenido de "Principio de d%27Alembert"